Dois blocos de massa e são conectados por uma corda inextensível sem massa por uma polia de massa e momento angular e raio , que gira em torno do seu eixo de simetria, em um plano inclinado com atrito dinâmico . O conjunto se move com se movendo para baixo e se movendo para cima. Considerando que a segunda lei de Newton fornece as equações do movimento de um corpo:
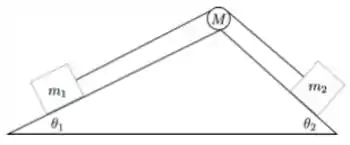
a) (1 ponto) Escreva a equação de movimento para os blocos de massa e ;
b) (1 ponto) Escreva a equação de movimento para a polia de massa ;
c) (1 ponto) A partir dos seus resultados nos itens anteriores, calcule a aceleração linear do sistema e as trações no fio;
Passo 1
a)
Nessa letra, a prova nos pede para escrever a equação do movimento para os nossos lindos blocos. Vamos então, fazer o Diagrama do Corpo Livre para cada um deles.
Mas antes, vamos dar uma olhada no enunciado. Lá diz que o bloco se move para cima e para baixo. Usaremos isso, para estipular a direção que será o positivo e a direção da força de atrito, ok ??
Ah, só mais uma coisinha. As trações não serão a mesma. Então iremos trabalhar com uma e . Isso ocorre por que a polia não é ideal. Beleza?
Então, bora lá. Vamos olhar o bloco
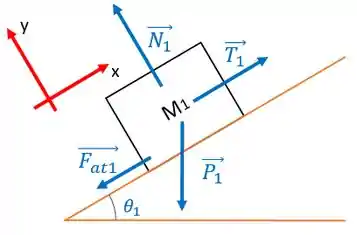
Primeira coisa que vamos fazer, é colocar esse peso na direção do plano inclinado:
Agora que decompomos o peso, é só aplicar Newton para cada direção.
Em y:
Em x:
Show, chegamos nessa expressão pro bloco . Partiu bloco ??
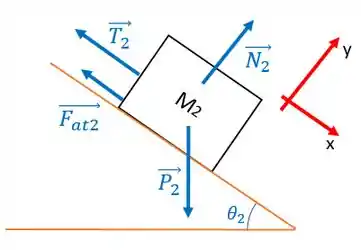
E repetindo os mesmos procedimentos, tudinho igual, vamos ter:
Em y:
Em x:
Passo 2
b)
Agora chegou a hora da polia brilhar.
A ideia é a mesma, aplicar a segunda lei de Newton, mas agora, queremos o caso rotacional.
First things first, bora de diagrama do corpo livre.
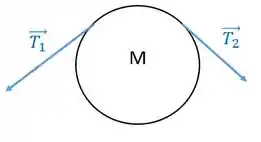
Sabemos que o movimento ocorre para a direita, logo a polia rotacional no sentido horário. Aplicando Newton:
Podemos relacionar a aceleração angular da polia com a aceleração linear dos blocos por meio de
Assim
Passo 3
c)
Então, essa questão aqui, ela só quer que você pegue tudo que você fez, e junta.
Nós temos que:
Se a gente subtrair...
E isso é justamente o que aparece do lado esquerdo da terceira equação. Assim
Agora temos “só” que isolar
E saiu esse bicho feio kkkk
Agora é só substituir essa nas primeira e segunda equações! Mas só substituir mesmo! Não precisa ficar quebrando cabeça pra ver se vai cortar alguma coisa hahaha
Resposta
a)
b)
c)