Uma máquina de Atwood possui massas , e uma polia maciça uniforme de massa M =2,0kg. O módulo da aceleração linear da massa vale:
a)
b)
c)
d)
e)
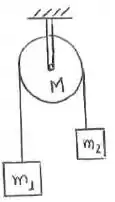
Passo 1
Isolando as forças, teremos:
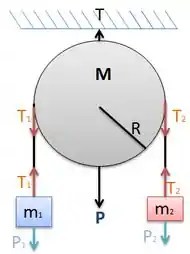
Duas forças em : e
Duas forças em : e
E quatro forças na Polia: (peso da polia), (reação pela polia estar presa ao teto), () e ( )
Passo 2
Vamos assumir que o bloco de massa está descendo e portanto se movimentando contra a orientação do nosso eixo vertical, então utilizando a segunda Lei de Newton para escrever as equações do movimento desse bloco, teremos:
Se o bloco desce, então o bloco sobe, teremos:
E não podemos esquecer de analisar o movimento de rotação da polia, já que a polia que faz parte do problema não é ideal. A polia não translada, mas pela Segunda Lei de Newton para rotação sabemos que e geram torque. Considerando a aceleração angular sendo positiva no sentido anti-horário, podemos escrever:
Passo 3
O da polia é dado por . Além disso, temos a relação .
Assim:
Passo 4
Agora montando um sistema com a equação do bloco de massa e do bloco , subtraindo a primeira da segunda, teremos:
Mas do Passo 3, pela equação do movimento de rotação da polia, sabemos que .
Substituindo na útima equação, teremos:
Passando para o outro lado, colocando em evidência, e substituindo os pesos por suas fórmulas correspondentes:
Isolando o :
Passo 5
Substituindo de vez agora os valores, teremos:
Como a aceleração do bloco é igual a , teremos:
Resposta
Letra D