Uma roldana tem a forma de um disco uniforme de massa e raio (ver figura). A roldana está presa ao teto e gira livremente ao redor do seu centro. Um fio ideal passa pela roldana sem deslizar. Este fio está preso aos blocos e , de modo que os módulos das tensões indicadas valem, respectivamente, e
Dados: Considere e utilize que o momento de inércia de um disco uniforme de massa e raio em relação ao eixo que passa no seu centro de massa e é perpendicular à sua superfície é .
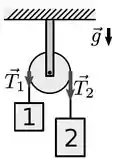
Calcule
- O módulo do torque devido à , em relação ao centro de massa da roldana
- O módulo da aceleração angular que a roldana está sujeita
Passo 1
Temos que o torque é dado por
Esse é o vetor que aponta do centro de rotação até o ponto onde a força atua. No nosso caso esse vetor é horizontal e dado por
E o vetor é um vetor vertical apontando para baixo
De forma que o torque fica
E seu módulo é dado por
Passo 2
Temos que a aceleração angular se relaciona com torque total por
Onde (dado pelo enunciado) é o momento de inércia.
Só que esse é o torque total, ou seja, devido às tensões e .
No item anterior, já calculamos a contribuição da tensão . Agora falta a o torque da tensão .
Dessa vez o vetor aponta para a esquerda, ou seja,
E o vetor aponta na direção vertical para baixo
De forma que
De forma que o torque total é dado por
Passo 3
Agora podemos calcular a aceleração angular
Resposta
(A)
(B)