Considere dois discos um de raio e de massa e outro de raio e de massa unidos concentricamente formando um sistema (disco composto) rígido, cujo momento de inércia vale quando gira livremente em torno do eixo fixo e perpendicular ao plano dos discos passando pelo centro. Duas massas, e , presas a cordas finas e inextensíveis enroladas na periferia dos discos de raios e respectivamente, fazem girar o disco composto quando soltas; considere que é o módulo da aceleração local da gravidade.
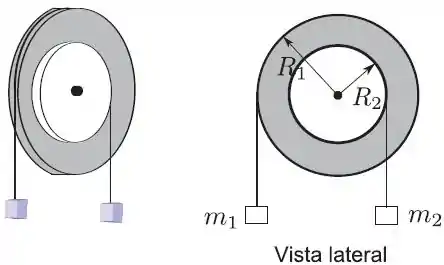
- Isole os blocos e o disco composto e represente em um diagrama de corpo livre todas as forças, identificando-as, que atuam em cada um deles; use como referência a vista lateral do sistema.
- Escreva as equações do movimento de rotação do disco composto e de translação dos blocos.
- Determine a aceleração angular, , do disco composto.
- Determine matematicamente a condição para que o sistema esteja em equilíbrio
Passo 1
a)
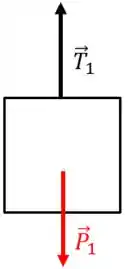
Vamos começar fazendo o DCL do bloco .
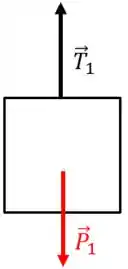
Nesse caso, só vamos ter a tração e a força peso atuando.
Passo 2
Agora no bloco será a mesma coisa que no bloco , só os pesos e as trações que são diferentes:
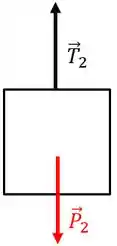
Passo 3
No disco, o DCL é o seguinte:
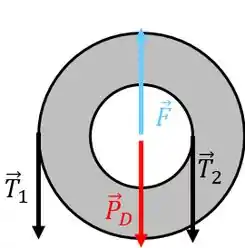
Nesse caso, temos as duas forças de tração, o peso do disco e a força de reação do pino que chamei de .
Passo 4
b)
Vamos considerar que o disco rola com aceleração angular no sentido anti-horário. É importante, em questões mais complexas como essa, olharmos a rotação do disco direito e com calma.
Vamos ter:
Então:
Passo 5
Se o disco está rolando no sentido anti-horário, o bloco está subindo e o bloco está descendo. Chamando cada módulo da aceleração de e , as equações do movimento serão as seguintes.
Para o bloco :
Lembrando que:
Resultando em:
Passo 6
Agora para o bloco :
Lembrando que:
Resultando em:
Passo 7
c)
Temos as seguintes equações:
Multiplicando a segunda equação por e a terceira equação por :
Agora somando todas as equações vamos ter:
Passo 8
Para que o sistema esteja em equilíbrio, devemos ter:
Então: