UFF – Sem campus – Física 1 – Provas antigas - VR – 8
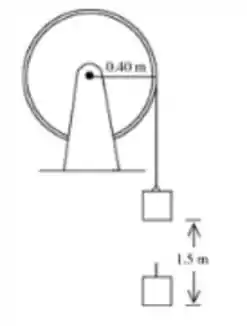
Um fio inextensível e de massa desprezível é enrolado em torno de uma polia de raio 0,40m. Um bloco amarrado na ponta deste fio é liberado do repouso, descendo 1,5 m em 2,0 segundos e fazendo a polia girar sem deslizamento do fio. Se a tensão na corda durante a descida do bloco vale 20 N, o momento de inércia da polia vale:
(A)
(B) 3.7 kg ·
(C) 3.9 kg ·
(D) 4.1 kg ·
(E) 4.3 kg ·
Passo 1
Fala turminha, tudo em cima? Bora lá resolver essa questão. Primeiro precisamos diagramar dentro de um sistema de coordenadas, pra facilitar nossa vida quando quisermos especificar certos pontos dentro do diagrama:
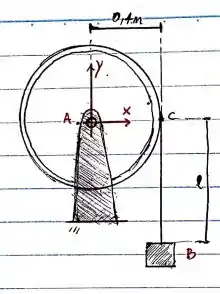
Para os diagramas de corpo livre separados:
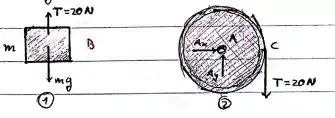
Passo 2
Beleza, agora que temos os diagramas de corpo livre separados, vamos descrever as velocidades para o ponto C pertencente a polia:
Show, com isso temos as equações descritas para velocidade e aceleração do bloco. Agora aplicando a segunda lei de newton para a força resultante:
Abrindo os termos:
Mas, g, T e m são constantes. Logo,
Passo 3
Agora vamos entender como o fio se comporta a medida que a polia gira. Encontramos isso através da cinemática. Para a cinemática do problema, temos que a nossa aceleração é dada por:
Logo, aplicando para a equação da posição e acharmos a diferença de tamanho das polias:
Para
E calculando os momentos na polia:
Logo,
Letra e). E é isso, ficamos por aqui! Se você gostou, ou ainda ficou alguma dúvida na questão, dá um feedback pra gente! Vamos adorar te responder