Conservação de energia mecânica
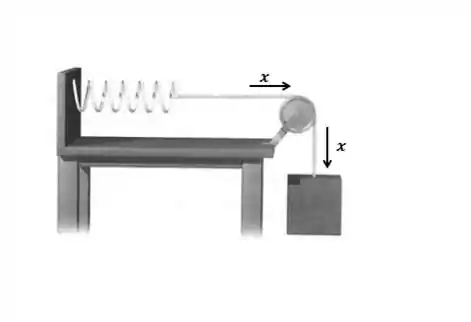
Um bloco de massa está preso a uma mola por uma corda inextensível e sem massa que passa por uma roldana de massa e raio , conforme mostrado na figura abaixo. A constante elástica da mola é . Trate a roldana como um disco maciço e homogêneo, despreze o atrito no eixo da roldana e assuma que o sistema parte do repouso com a mola não distendida.
Dado: Momento de inércia da roldana:
- A velocidade do bloco após ele cair
- A distensão máxima da mola.
Passo 1
a
Bom, galera, como o bloco cai metros, a mola vai se distender também em metros:
Então, pela conservação da energia mecânica, a energia potencial da altura que o bloquinho tinha, virará energia potencial elástica e cinética:
Hum, mas ali também tem uma energia de rotação, da roldana.
Essa energia de rotação é dada por:
Nesse caso, podemos dizer que a rotação acontece sem deslizamento, então:
E o momento de inércia é dado por:
Então:
Assim:
Substituindo os valores que sabemos:
Pronto!
Passo 2
b)
A distensão máxima da mola ocorre quando a força da mola equilibra o peso do corpo:
Resposta
a)
b)