Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Polias Não-Ideais

Ver Teoria
Exercício 4312345678910111213141516171819202122232425262728293031323334353637383940414244454647

Enunciado

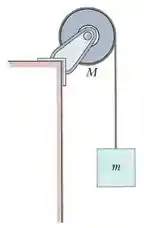
Uma roldana de massa M e raio R está montada num eixo horizontal sem atrito. O momento de inércia da roldana em relação ao eixo de rotação é I   =   M R 2 / 2 . Uma corda de massa desprezível está enrolada na roldana. Na extremidade livre da corda está suspenso um bloco de massa m . A corda não desliza em relação à roldana. O sistema é liberado a partir do repouso. Enquanto o bloco desce qual é a tensão na corda?

(A) m M m + 2 M g

(B) m R m + M g

(C) m 2 2 m + M g

(D) m M 2 m + M g

(E) m M 2 m + M R 2 g

Passo 1

Temos que o torque sobre a roldana devido a tração do fio é dado por

τ = T R

Pela segunda lei para rotações temos que

τ = I α

Assim

I α = T R → α = T R I

Por outro lado, temos que a aceleração angular da roldana se relaciona com a aceleração linear do fio por

a = α R

De forma que

a = T R 2 I

Passo 2

Agora se escrevermos a segunda lei de Newton para o bloco de massa m , temos

m a = m g - T

Onde a é a mesma aceleração tanto para o bloco quanto para o fio. Substituindo pelo valor de a que achamos antes temos que

m T R 2 I = m g - T → T + m T R 2 I = m g

T 1 + m R 2 I = m g

Substituindo I = M R 2 / 2 (dado pelo enunciado)

T 1 + m R 2 M R 2 2 = m g → T 1 + 2 m M = m g

T M + 2 m M = m g

T = m M M + 2 m g

Resposta

(D)

Exercícios de Livros Relacionados

Um dispositivo para medir o momento de inércia de um corpo é mostrado na figura. A plataforma circular está presa a um tambor concêntrico de raio R , plataforma e tambor estando livres para girar em t
Um cilindro de uniforme, de massa M e raio R , tem um fio enrolado no seu entorno. O fio é mantido fixo, enquanto o cilindro cai verticalmente, como mostrado na figura. (a) Mostre que a aceleração do
A extremidade superior do fio enrolado em redor do cilindro da figura está segura por uma mão que acelera para cima, de modo que o centro de massa do cilindro não se move, enquanto o cilindro gira. De
Calcule o efeito da massa M da polia, de raio R , sobre o sistema do Cap. 4, Probl. 12 (fig); a masssa m , que desliza sem atrito está ligado à massa suspensa m ' pelo fio que passa sobre a polia. Det
Um bloco de massa m , que pode deslizar com atrito desprezível sobre um plano inclinado de inclinação θ em relação à horizontal, está ligado por um fio, que passa sobre uma polia de raio R e massa M ,