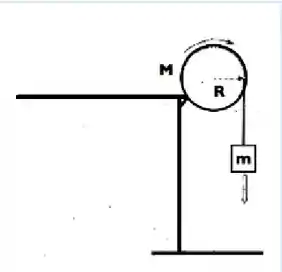
Um bloco de massa , suspenso por uma polia de raio e massa , é solto a partir do repouso. Considere a polia como um disco de densidade uniforme. Qual é a aceleração do bloco?
a)
b)
c)
d)
e)
Passo 1
Questão pediu aceleração. Já vou desconfiar que aqui eu tenho que aplicar segunda lei de Newton. Vamos fazer isso para os nossos dois corpos, tá bom? Então, tá bom.
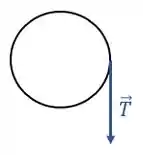
Polia
Bloco
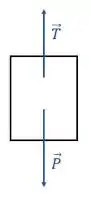
Agora, unindo as duas equações, teremos:
Mas repara só, a aceleração do bloco é a mesma aceleração tangencial da extremidade da polia.
E podemos relacionar essa aceleração com a aceleração angular.
Substituindo, teremos finalmente:
Resposta
Letra b)
Exercícios de Livros Relacionados
Um dispositivo para medir o momento de inércia de um corpo é mostrado na figura. A plataforma circular está presa a um tambor concêntrico de raio R , plataforma e tambor estando livres para girar em t
Um cilindro de uniforme, de massa M e raio R , tem um fio enrolado no seu entorno. O fio é mantido fixo, enquanto o cilindro cai verticalmente, como mostrado na figura. (a) Mostre que a aceleração do
A extremidade superior do fio enrolado em redor do cilindro da figura está segura por uma mão que acelera para cima, de modo que o centro de massa do cilindro não se move, enquanto o cilindro gira. De
Calcule o efeito da massa M da polia, de raio R , sobre o sistema do Cap. 4, Probl. 12 (fig); a masssa m , que desliza sem atrito está ligado à massa suspensa m ' pelo fio que passa sobre a polia. Det
Um bloco de massa m , que pode deslizar com atrito desprezível sobre um plano inclinado de inclinação θ em relação à horizontal, está ligado por um fio, que passa sobre uma polia de raio R e massa M ,