Dois blocos de massas e estão conectados por um fio ideal, como mostrado na figura. Se o raio da polia é de e seu momento de inércia em relação ao eixo de rotação é igual a , qual é o módulo da aceleração de cada um dos blocos (em função da aceleração da gravidade )?
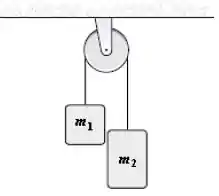
(A)
(B)
(C)
(D)
(E)
Passo 1
Nessa questão, a polia é não-ideal. Isso significa que ela apresenta uma massa e um momento de inércia que não são desprezíveis.
Então, além de aplicar a Segunda Lei de Newton para os dois blocos, temos que aplicar também a Segunda Lei de Newton para rotações na polia.
Além disso, como os dois blocos estão presos por uma mesma corda, eles se movimentam juntos. Logo, as suas acelerações são iguais em módulo:
Passo 2
Começando com os blocos.
O bloco 2 é mais pesado que o bloco 1, por isso está descendo (aceleração para baixo):
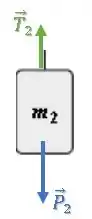
Já o bloco 1, está sendo puxado para cima (aceleração para cima):
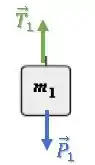
Passo 3
Agora, vamos aplicar a Segunda Lei de Newton para rotação na polia.
Primeiro de tudo, as forças na polia são:
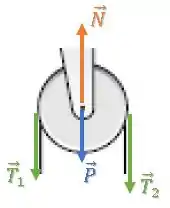
A força peso e normal estão aplicadas no eixo de rotação da polia, então não geram torque.
Vamos focar apenas nas duas forças de tração.
Os vetores posição apresentam módulo igual ao raio da polia e são perpendiculares aos vetores de tração.
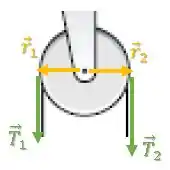
A polia gira no sentido horário.
Vamos considerar o sentido horário positivo, então os torque serão:
Se não há deslizamento entre o cabo e a polia, podemos usar a seguinte relação:
Substituindo isso na expressão:
Passo 4
Ficamos com esse sisteminha aqui:
Nosso objetivo é achar a aceleração . Então, vamos sumir com as forças de tração (incógnitas).
Primeiro vamos somar a primeira e a terceira equação:
Agora vamos somar a segunda equação com essa expressão:
Passo 5
Substituindo os valores:
Ficamos com a letra (C).
Resposta
Letra (C)