UFJF – Cálculo 1 – AV2 – 2019/2
1. Considere um ângulo tal que . O valor de é:
a)
b)
c)
d)
e)
Passo 1
Falaaaa... beleza??
Nessa questão queremos achar o valor de sabendo que e que o ângulo está no intervalo
Pra isso vamos usar a identidade trigonométrica:
E também usar o círculo trigonométrico pra dizer qual é o sinal.
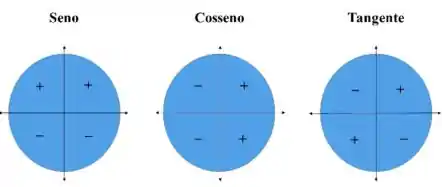
Passo 2
Temos que . Usando a identidade trigonométrica:
Cuidadoooo, heim??? Quando a gente vai passar o quadrado pro outro lado como raiz precisamos lembrar que é + ou -...
Passo 3
Agora usamos o intervalo dado pra descobrir se é mais ou se é menos.
Como o intervalo é , então sabemos que está no segundo quadrante. Olhando para o círculo trigonométrico, temos que o cosseno no segundo quadrante tem valores negativos, então:
Letra c
Resposta
Letra c
Exercícios de Livros Relacionados
Calcule o valor da expressão s e n 105 ° - c o s 75 ° .
Calcule cotg 165°, sec 255° e cossec 15°.
Sejam α = a r cs e n 4 5 um arco no 2º quadrante e β = a r ct g - 4 3 um arco no 4º quadrante. Calcule 25 c o s ( α + β ) .
Determine os seguintes números: a r c t g 0 , a r c t g sqrt(3) , a r c t g (- 1) , a r c t g ((- sqrt(3))/(3)) .
Calcule:a ) s e n (a r c t g 2 + a r c t g 3) . b ) cos (a r c t g 2 - a r c t g (1)/(2)) . c ) t g (2 a r c t g (1)/(5)) . d ) cos (3 a r c t g (24)/(7)) .