UFSC, Sem Campus, Pré-Cálculo, Listas Pré-Cálculo - Lista 14, Questão 2
A função dada por é bijetora (verifique através gráfico) e, portanto, possui inversa. Sua inversa é denotada por (às vezes também é denotada por ). Por exemplo, é igual ao único número pertencente a cujo seno é igual a e, portanto, . Como outros exemplos, temos e (compare com as equações resolvidas no exercício anterior). Calcule o que se pede
Passo 1
Eaew, belezinha?
O enunciado basicamente nos descreve o que é uma função inversa, em particular discutindo o arcoseno que será útil nesta questão, e pede para calcularmos
Para isso, vamos usar propriedades da função e alguns valores conhecidos! Belezinha? Bora lá!
Passo 2
Primeiro temos , precisamos encontrar o ângulo no qual o , o gráfico do seno é o seguinte
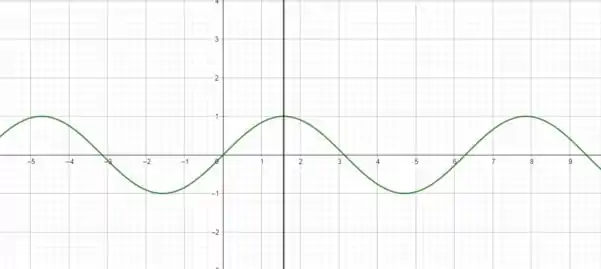
eu marquei ali o valor de , portanto, temos que para , e portanto
Vamos fazer uma análise análoga para as outras alternativas!
Passo 3
Agora para , você lembra daquela tabelinha de ângulos conhecidos para seno, cosseno e tangente, ela era tal que
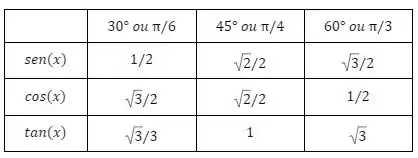
note que o portanto, temos que
com a tabela já podemos identificar também que
Faltam mais três! Mas para esses, vamos precisar lembrar de uma propriedade da função ! Saca só!
Passo 4
Temos que a função seno é uma função com paridade ímpar, portanto, temos que
Portanto, se eu considero o valor de , temos que
Portanto, se queremos , iremos estar procurando o ângulo , resumindo
da mesma forma podemos usar a tabela junto com esta propriedade e obter que
e
A questão foi isso! Te vejo na próxima! Tchau Tchau!