Considere o círculo de raio desenhado no plano cartesiano com centro na origem. Quando caminhamos uma distância sobre o círculo a partir do ponto no sentido anti-horário, o ponto final do trajeto é denominado ponto terminal de . Por exemplo, como o círculo tem comprimento , então o ponto terminal de , o ponto terminal de e o ponto terminal de . Se é negativo, devemos andar no sentido horário. Por exemplo, o ponto terminal de. Determine o ponto terminal dos valores de abaixo.

Fala galera, tudo beleza? Vamos para mais uma questão de pré-cálculo . Nosso objetivo é Determinar os pontos terminais para os valores de . A definição dada no enunciado é meio estranha. Mas ela basicamente quer dizer que o ponto terminal é o ponto onde o angûlo formado entre o raio do círculo e a horizontal é de radianos

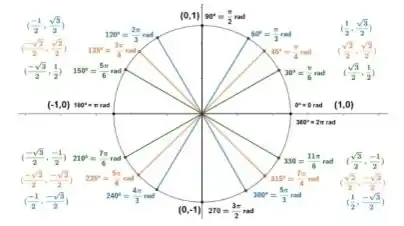
Nesse caso, temos que as coordenadas do ponto serão . Com isso em mente, vamos começar pela letra

Então, como comentamos temos que as coordenadas do ponto terminal são

Letra

As coordenadas do ponto terminal são

Letra

As coordenadas do ponto terminal são

Letra

As coordenadas do ponto terminal são

Letra

As coordenadas do ponto terminal são

Letra

As coordenadas do ponto terminal são

Letra

As coordenadas do ponto terminal são

Letra

As coordenadas do ponto terminal são

Prontinho pessoal!! Finalizamos mais uma questão. Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊