Quanto vale o ?
- 1
Passo 1
Vamos láá!! Como podemos calcular o de um ângulo que não está no primeiro quadrante??
Calma meu pupilo!!! Vamos ver que calcular o desses valores não é difícil!! Basta a gente observar a simetria do círculo trigonométrico. Primeiro vamos olhar para o ângulo de no círculo trigonométrico:
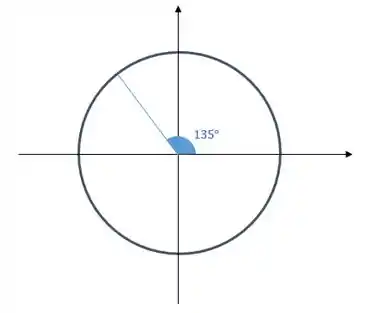
Note que esse ângulo de , para chegar a , está faltando , beleza?!
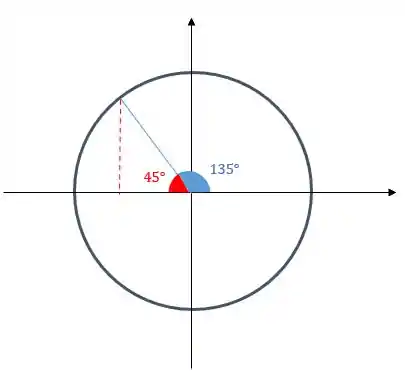
Show de bola?!
Passo 2
Como o ângulo de está no segundo quadrante, repare que o que é sempre dado no eixo é negativo... (Uma dica é lembrar que o está com sono, então ele está de pé rs)
Assim,
Se olharmos para a nossa tabelinha dos ângulos notáveis, podemos encontrar o valor de
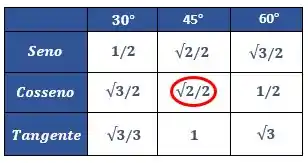
Ou seja,
Show de bola?!
Resposta
Exercícios de Livros Relacionados
Calcule o valor da expressão s e n 105 ° - c o s 75 ° .
Calcule cotg 165°, sec 255° e cossec 15°.
Sejam α = a r cs e n 4 5 um arco no 2º quadrante e β = a r ct g - 4 3 um arco no 4º quadrante. Calcule 25 c o s ( α + β ) .
Determine os seguintes números: a r c t g 0 , a r c t g sqrt(3) , a r c t g (- 1) , a r c t g ((- sqrt(3))/(3)) .
Calcule:a ) s e n (a r c t g 2 + a r c t g 3) . b ) cos (a r c t g 2 - a r c t g (1)/(2)) . c ) t g (2 a r c t g (1)/(5)) . d ) cos (3 a r c t g (24)/(7)) .