Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Círculo Trigonométrico

Ver Teoria
Exercício 21123456789101112131415161718192022232425262728293031323334353637383940414243

Enunciado

UFSC, Sem Campus, Pré-Cálculo, Listas Pré Cálculo - Lista 14, Questão 1

Resolva as equações abaixo

  1.   s e n   x   =   0 .
  2. s e n   x   =   1 .
  3. s e n   x   = 1 / 2
  4. s e n   x   =   0 ,   x   ∈   [ − π / 2 ,   π / 2 ] .
  5. s e n   x   =   1 ,   x   ∈   [ − π / 2 ,   π / 2 ]
  6. s e n   x   = 1 / 2   ,   x   ∈   [ − π / 2 ,   π / 2 ] .

Passo 1

Fala galera, tudo beleza? Vamos para mais uma questão de pré-cálculo . Nosso objetivo é calcular as equações. Para isso, vamos dar u8ma relembrada no ciclo trigonométrico

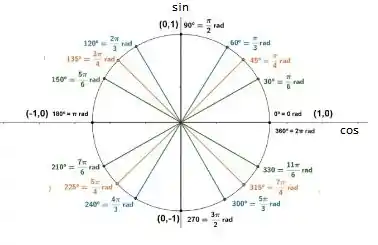
Show? Então vamos começar pela letra a )

  s e n   x   =   0 .

Bem, como o s i n ( x ) é uma função periódica, temos que ela vai assumir o valor zero sempre que x for um múltiplo de π . Logo,

  s e n   x   =   0

⇒ x = π k ,   k ∈ Z

Letra b )

s e n   x   =   1

Bem, como o s i n ( x ) é uma função periódica, temos que ela vai assumir o valor um sempre que x for π / 2 , mas podemos encontrar mais valores que satisfazem ao darmos uma volta completa na circunferência. Logo,

s e n   x   =   1

⇒ x = π / 2 + k 2 π ;   k ∈ Z

Letra c )

s e n   x   = 1 / 2

Essa é um seno famoso é o de π / 6 . mas também é do 5 π / 6 . Mas podemos encontrar mais valores que satisfazem ao darmos uma volta completa na circunferência. Ou seja

s e n   x   = 1 / 2

⇒ x = π / 6 + k 2 π ;   k ∈ Z

ou

x = 5 π / 6 + k 2 π ;   k ∈ Z

Letra d )

s e n   x   =   0 ,   x   ∈   [ − π / 2 ,   π / 2 ]

Como vimos na letra a

  s e n   x   =   0

⇒ x = π k ,   k ∈ Z

Mas como   x   ∈   [ − π / 2 ,   π / 2 ] , então

x = 0

Letra e )

s e n   x   =   1 ,   x   ∈   [ − π / 2 ,   π / 2 ]

como vimos na letra b

  s e n   x   =   1

⇒ x = π / 2   +   2 π k ,   k ∈ Z

Mas como   x   ∈   [ − π / 2 ,   π / 2 ] , então

x = π / 2

ou

x = - π / 2

Letra f )

s e n   x   = 1 / 2   ,   x   ∈   [ − π / 2 ,   π / 2 ] .

como vimos na letra c

  s e n   x   =   1 / 2

⇒ x = π / 6   +   2 π k ,   k ∈ Z

ou

x = 5 π / 6   +   2 π k ,   k ∈ Z

Mas como   x   ∈   [ − π / 2 ,   π / 2 ] , então

x = π / 6

Prontinho pessoal!! Finalizamos mais uma questão. Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊

Resposta

Desenvolvimento acima

Exercícios de Livros Relacionados

Calcule o valor da expressão s e n 105 ° - c o s 75 ° .
Calcule cotg 165°, sec 255° e cossec 15°.
Sejam α = a r cs e n 4 5 um arco no 2º quadrante e β = a r ct g - 4 3 um arco no 4º quadrante. Calcule 25 c o s ⁡ ( α + β ) .
Determine os seguintes números: a r c t g 0 , a r c t g sqrt(3) , a r c t g (- 1) , a r c t g ((- sqrt(3))/(3)) .
Calcule:a ) s e n (a r c t g 2 + a r c t g 3) . b ) cos (a r c t g 2 - a r c t g (1)/(2)) . c ) t g (2 a r c t g (1)/(5)) . d ) cos (3 a r c t g (24)/(7)) .