Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Círculo Trigonométrico

Ver Teoria
Exercício 17123456789101112131415161819202122232425262728293031323334353637383940414243

Enunciado

UFSC, Sem Campus, Pré-Cálculo, Listas Pré Cálculo - Lista 13, Questão 14

Determine o valor das outras funções trigonométricas em t , sabendo o valor de uma delas e o quadrante do terminal de t .

(a) s e n   t   =   3 / 5 com terminal de t no segundo quadrante.

(b) c o s t   =   - 1 / 5   com terminal de t no terceiro quadrante.

(c) t g �� t   =   - 7   com terminal de t no quarto quadrante.

(d) c o t g   t   =   2 / 3 com terminal de t no primeiro quadrante.

(e) s e c   t   =   - 2 com terminal de t no segundo quadrante.

(f) c o s s e c   t   =   - 5 / 4 com terminal de t no quarto quadrante.

Passo 1

Fala galera, tudo beleza? Vamos para mais uma questão de pré-cálculo . Nosso objetivo é encontrar o valor das demais funções trigonométricas s i n , c o s .

lembrando que o ponto terminal é o ponto onde o ângulo formado entre o raio do círculo e a horizontal é de t radianos

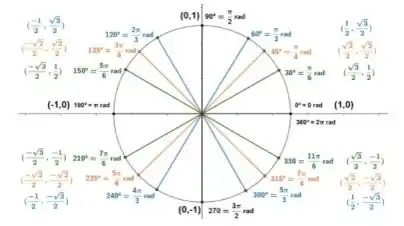
Vamos começar pela letra a )

Como t está no segundo quadrante, temos que s i n ( t ) > 0 e c o s ( t ) < 0 . Usando a relação de seno e cosseno temos que

s i n 2 ( t ) + c o s 2 ( t ) = 1

⇒ c o s 2 ( t ) = 1 - s i n 2 ( t )

⇒ c o s ( t ) = - 1 - s i n 2 ( t )

pois c o s ( t ) < 0

Logo, como s e n   t   =   3 / 5

c o s ( t ) = - 1 - 9 / 25

= - 4 / 5

letra b )

Como t está no terceiro quadrante, temos que s i n ( t ) < 0 e c o s ( t ) < 0 . Usando a relação de seno e cosseno temos que

s i n 2 ( t ) + c o s 2 ( t ) = 1

⇒ s i n 2 ( t ) = 1 - c o s 2 ( t )

⇒ s i n ( t ) = - 1 - c o s 2 ( t )

pois s i n ( t ) < 0

Logo, como c o s t   =   - 1 / 5  

s i n ( t ) = - 1 - 1 / 25

= - 24 / 25

letra c )

Como t está no quarto quadrante, temos que s i n ( t ) < 0 e c o s ( t ) > 0 . Mas só podemos inferir isso. Pois são temos que t g   t   =   - 7  

letra d )

Como t está no primeiro quadrante, temos que s i n ( t ) > 0 e c o s ( t ) > 0 . mas só podemos inferir isso, pois

c o t g   t   =   2 / 3

⇒ t g   t   =   3 / 2

letra e )

Como t está no segundo quadrante, temos que s i n ( t ) > 0 e c o s ( t ) < 0 . Usando a relação de seno e cosseno temos que

s i n 2 ( t ) + c o s 2 ( t ) = 1

⇒ s i n 2 ( t ) = 1 - c o s 2 ( t )

⇒ s i n ( t ) = 1 - c o s 2 ( t )

pois s i n ( t ) > 0

Logo, como s e c   t   =   - 2

temos que

c o s = - 1 / 2

então

s i n ( t ) = 1 - 1 / 4

= 3 / 2

letra f )

Como t está no quarto quadrante, temos que s i n ( t ) < 0 e c o s ( t ) > 0 . Usando a relação de seno e cosseno temos que

s i n 2 ( t ) + c o s 2 ( t ) = 1

⇒ c o s 2 ( t ) = 1 - s i n 2 ( t )

⇒ c o s ( t ) = 1 - s i n 2 ( t )

pois c o s ( t ) > 0

Logo, como c o s s e c   t   =   - 5 / 4

temos que

s i n = - 4 / 5

então

c o s ( t ) = 1 - 16 / 25

= 3 / 5

Prontinho pessoal!! Finalizamos mais uma questão. Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊

Resposta

Desenvolvimento acima

Exercícios de Livros Relacionados

Calcule o valor da expressão s e n 105 ° - c o s 75 ° .
Calcule cotg 165°, sec 255° e cossec 15°.
Sejam α = a r cs e n 4 5 um arco no 2º quadrante e β = a r ct g - 4 3 um arco no 4º quadrante. Calcule 25 c o s ⁡ ( α + β ) .
Determine os seguintes números: a r c t g 0 , a r c t g sqrt(3) , a r c t g (- 1) , a r c t g ((- sqrt(3))/(3)) .
Calcule:a ) s e n (a r c t g 2 + a r c t g 3) . b ) cos (a r c t g 2 - a r c t g (1)/(2)) . c ) t g (2 a r c t g (1)/(5)) . d ) cos (3 a r c t g (24)/(7)) .