UFSC, Sem Campus, Pré-Cálculo, Listas Pré Cálculo - Lista 13, Questão 15
Sabendo que o ponto terminal de está no segundo quadrante, escreva em função de
Passo 1
Fala galera, tudo beleza? Vamos para mais uma questão de pré-cálculo . Nosso objetivo é escrever em função de . Sabendo que o ponto terminal de está no segundo quadrante.
lembrando que o ponto terminal é o ponto onde o ângulo formado entre o raio do círculo e a horizontal é de radianos
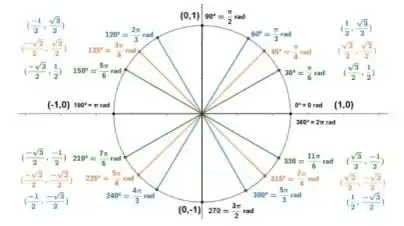
Como está no segundo quadrante, temos que e . Usando a relação de seno e cosseno temos que
pois
Logo, temos que
Prontinho pessoal!! Finalizamos mais uma questão. Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊
Resposta
Desenvolvimento acima
Exercícios de Livros Relacionados
Calcule o valor da expressão s e n 105 ° - c o s 75 ° .
Calcule cotg 165°, sec 255° e cossec 15°.
Sejam α = a r cs e n 4 5 um arco no 2º quadrante e β = a r ct g - 4 3 um arco no 4º quadrante. Calcule 25 c o s ( α + β ) .
Determine os seguintes números: a r c t g 0 , a r c t g sqrt(3) , a r c t g (- 1) , a r c t g ((- sqrt(3))/(3)) .
Calcule:a ) s e n (a r c t g 2 + a r c t g 3) . b ) cos (a r c t g 2 - a r c t g (1)/(2)) . c ) t g (2 a r c t g (1)/(5)) . d ) cos (3 a r c t g (24)/(7)) .