UFSC – Pré Cálculo – Exame – Questão 15
Sabendo que , qual dos valores abaixo pode ser igual a ?
Passo 1
E aí pessoal, tudo bem?
Essa questão parece complicada, mas vou ajudar você aqui!
O problema pediu para a partir de um valor de tangente, acharmos um possível valor seno desse mesmo ângulo!
Mas calma! A ideia aqui é lembrar da definição geométrica de tangente!
E a partir daqui construir um triângulo para achar a hipotenusa! E o que fazer com isso? Te conto a seguir!
Mas relaxa, vou fazer passo a passo com você!
Passo 2
Como comentei ali no passo 1, com a tangente temos indiretamente os valores (em módulo) dos lados de um triângulo
Vamos supor um triângulo assim
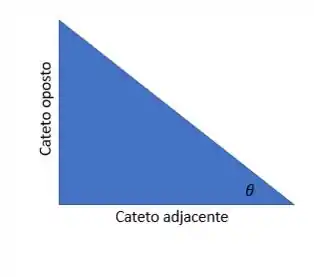
Do enunciado temos que a tangente
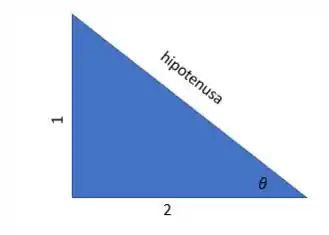Então em módulo temos
assim temos as medidas completas do triângulo, em relação ao ângulo
Beleza até aqui?
Passo 3
Agora vem o pulo do gato! Sabendo o cateto oposto e a hipotenusa, conseguimos achar o seno desse ângulo?
SIM!
E é isso que vamos fazer:
Mas sabemos que o seno pode assumir valores positivos e negativos, então nesse ângulo
E nas alternativas temos apenas o valor positivo! Então essa é nossa resposta! Caso tivesse o valor positivo E o negativo, o exercício precisaria dar o quadrante que o seno está, assim podemos ver se ele é positivo ou negativo
E é isso! A alternativa correta é (C)
Espero ter ajudado! Vamos para a próxima?