Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Círculo Trigonométrico

Ver Teoria
Exercício 31123456789101112131415161718192021222324252627282930323334353637383940414243

Enunciado

UFSC, Sem Campus, Pré-Cálculo, Listas Pré Cálculo - Lista 14, Questão 16

Observe os gráficos das funções trigonométricas e verifique quais são pares e quais são ímpares. A partir disso, reescreva as expressões abaixo, conforme item (a).

  1. s e n ( − x )   =   −   s e n   x , isto é, a função seno é ímpar.
  2. c o s ( − x ) .
  3. t g ( − x ) .
  4. c o t g ( − x ) .
  5. s e c ( − x ) .
  6. c o s s e c ( − x ) .

Passo 1

Fala galera, tudo beleza? Vamos para mais uma questão de pré-cálculo . Nosso objetivo é

verificar se as funções seno e cosseno são pares ou ímpares e reescrever as expressões seguindo esse critério de paridade

Vamos relembrar a definição de paridade de uma função.

Dizemos que uma função f ( x ) é par se

f ( - x ) = f ( x )

E dizemos que é ímpar se

f ( - x ) = - f ( x )

Com isso em mente, vamos olhar os gráficos do seno e cosseno, respectivamente, abaixo

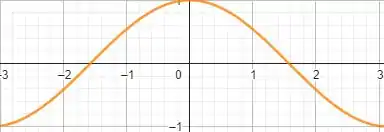
Ao analisarmos os gráficos, podemos chegar a conclusão que o seno é uma função ímpar, e o cosseno é uma função par

Passo 2

Agora que sabemos a paridade das funções seno e cosseno, vamos fazer a letra letra b )

c o s ( − x ) = c o s ( x ) ,   p o i s   c o s s e n o   é   p a r

letra c )

t g ( − x ) = s i n ( - x ) / c o s ( - x )

como o seno é ímpar e o cosseno é par

= - s i n ( x ) / c o s ( x )

= - t g ( x )

Logo tangente é uma função ímpar

letra d )

c o t g ( − x )

c o t g ( − x ) = 1 / t g ( - x )

como vimos na letra c ) . Tangente é função ímpar. então

c o t g ( − x ) = 1 / t g ( - x )

= - 1 / t g ( x )

= - c o t g ( x )

Logo,

c o t g ( − x ) = - c o t g ( x )

letra e )

s e c ( − x )

Como

s e c ( − x ) = 1 / c o s ( - x )

e como o cosseno é uma função par. Temos:

s e c ( − x ) = 1 / c o s ( - x )

= 1 / c o s ( x )

= s e c ( x )

Ou seja, a função secante é par

letra f )

c o s s e c ( − x ) .

Como

c o s s e c ( − x ) = 1 / s i n ( - x )

e como o seno é uma função ímpar. Temos:

c o s s e c ( − x ) = 1 / s i n ( - x )

= - 1 / s i n ( x )

Logo

c o s s e c ( − x ) = - c o s s e c ( x )

Ou seja, a cossecante é uma função ímpar

Prontinho pessoal!! Finalizamos mais uma questão. Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊

Resposta

Desenvolvimento acima

Exercícios de Livros Relacionados

Calcule o valor da expressão s e n 105 ° - c o s 75 ° .
Calcule cotg 165°, sec 255° e cossec 15°.
Sejam α = a r cs e n 4 5 um arco no 2º quadrante e β = a r ct g - 4 3 um arco no 4º quadrante. Calcule 25 c o s ⁡ ( α + β ) .
Determine os seguintes números: a r c t g 0 , a r c t g sqrt(3) , a r c t g (- 1) , a r c t g ((- sqrt(3))/(3)) .
Calcule:a ) s e n (a r c t g 2 + a r c t g 3) . b ) cos (a r c t g 2 - a r c t g (1)/(2)) . c ) t g (2 a r c t g (1)/(5)) . d ) cos (3 a r c t g (24)/(7)) .