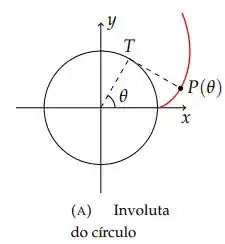
Um barbante é enrolado ao redor de um círculo e então desenrolado, sendo mantido esticado. A curva traçada pelo ponto P no final do barbante é chamada de involuta do círculo. Se o círculo tiver raio r e centro O, a posição inicial de P for (r, 0), e se o parâmetro θ for escolhido como na Figura 1(a), mostre que as equações paramétricas da involuta são:
e
Passo 1
Eaew, belezinha?
Temos que chegar nas equações paramétricas da involuta:
e .
Olhando para a figura temos dois triângulos, e :
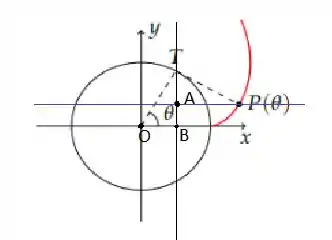
Como o segmento de barbante , que foi desenrolado, está sempre tangenciando o círculo, temos que o ângulo é igual ao ângulo . Assim, temos que as coordenadas do ponto P serão dadas pela soma ou subtração dos catetos dos triângulos.
Vamos lá!
Passo 2
Olhando novamente para a figura
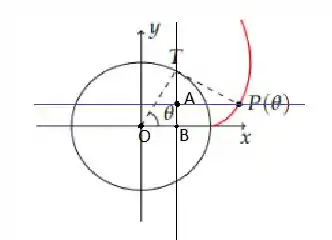
Temos que:
Então, as equações paramétricas da involuta são:
e .
A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
No decorrer da questão.