UFPE – Cálculo 1 – Listas de C1 - MQCC1 – 2ª Lista – 2023.1 – Exercício 2c
Escrever uma equação para a reta r, nos seguintes casos:
c) r é a bissetriz do 2° e 4° quadrantes.
Passo 1
Fala aí galera, bora resolver o nosso exercício? Vamos lá.
Bom, para montarmos a equação da reta, precisamos analisar por onde passa a reta e interpretar.
Para isso, temos que relembrar a fórmula geral de uma reta:
Show, e com isso vamos atrás de cada componente e montar a nossa reta.
Passo 2
Fala aí galera, bora resolver o nosso exercício? Vamos lá.
Bom, o enunciado nos diz que:
O que isso significa? Bom, quando uma reta é a bissetriz de algo, significa que ela divide o ângulo disso em 2 iguais. Como ela é a bissetriz do 2º e 4º quadrante, vamos ter algo assim:
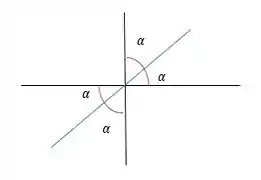
Como cada quadrante tem o ângulo total de 90º, a bissetriz divide esse ângulo em dois iguais, então podemos dizer que:
Ok, já temos o ângulo, mas como que achamos a reta pedida pelo enunciado? No passo 1 vimos que a fórmula geral é:
Show, mas além disso, temos que lembrar que:
Logo,
Porém, reparem que o enunciado pede referente ao 2º e 4º quadrante, logo precisamos multiplicar por -1, então:
Beleza, agora temos que achar o valor de . Bom, o enunciado diz que a nossa reta é a bissetriz dos nossos quadrantes. Para ela ser bissetriz, ela divide os quadrantes em partes iguais, logo ela precisa passar pela origem.
Quando uma reta passa pela origem, significa que ela não tem deslocamento, logo:
Encontrando: