UFF, Sem Campus, Cálculo IIB, P1 - Prof. Jorge Delgado - 2023 - Verão, Questão 3a.
3 – Considere a função .
a) Desenhe e dê as equações cartesianas das curvas de nível e de nível da função .
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉
Nesse problema queremos obter as curvas de níveis para a função para os níveis e .
Tem ideia de como podemos fazer isso? 🤔
Para obter as curvas de níveis de uma função, temos que substituir pelo nível que estamos interessados.
Isso porque resulta na imagem da função, como já temos a imagem, vamos atras da função...
Entendeu? Bora começar! 😁
Passo 2
Primeiro para o nível , temos
Isolando , vamos obter
Portanto essa é a fun��ão que quando esboçada no plano nos dá a curva de nível em .
Analisando essa equação, vemos que conforme tende a , tende a infinito e conforme aumenta, tende a ... ou seja
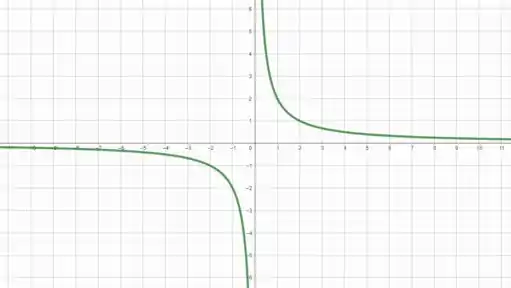
Tranquilo até aqui? 😉
Passo 3
Agora para o nível fazemos o mesmo procedimento
Analisando a função, vemos que obtemos características contrarias... quando tende a a função tende a e para muito grande, a função tende a novamente...
Veja só
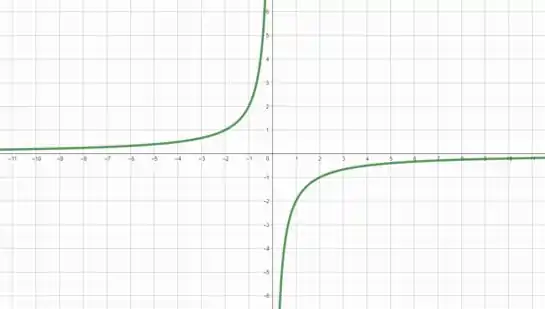
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍
