UFU, Sem Campus, Cálculo 2, Listas de Cálculo 2 - Profº M. C. Fenille – Segunda Lista de Exercícios, Questão 8
A função dada por parametriza uma curva que está sobre uma superfície de equação . Obtenha tal equação e esboce a superfície. Na mesma figura, esboce a curva e, ainda, detaque o ponto e esboce o vetor .
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado nos deu uma curva parametrizada e quer que a gente encontre a equação catersiana que está sob a curva que deu origem a essa parametrização. Em seguida, esboçar a curva junto com o vetor derivada de e o ponto .
Esse é o caminho inverso ao que geralmente fazemos quando precisamos parametrizar uma curva. Agora nós queremos descobrir a equação da curva que foi parametrizada. Para isso, vamos encontrar uma relação cartesiana entre as componentes do vetor . No nosso caso, temos:
Assim, usando a identidade trigonométrica , conseguimos definir uma relação cartesiana. Com isso, vamos plotar a curva em um gráfico e marcar os pontos que a questão pediu.
Vamos lá!
Passo 2
Vamos começar observando nosso vetor . Repare que, pela relação trigonométrica ():
Para todo . Dessa forma, nossa curva estará acima da superfície do cone:
Isso significa que a nossa curva será uma curva helicoidal cônica, porque ela vai “percorrendo” a superfície do cone.
Com a ajuda de um software, a gente consegue plotar o cone usando a equação dessa superfície que nós encontramos, . Em seguida, nós plotamos a curva (em preto), usando o vetor , onde o parâmetro que varia de a , como foi definido no enunciado. Assim, nós temos:
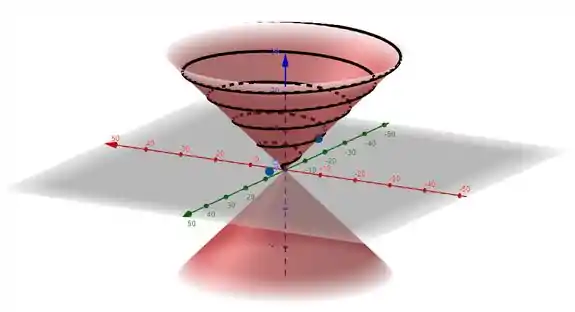
Repare nos pontos e em azul. O ponto representa , que a gente calcula substituindo na equação:
Assim,
E o ponto representa a derivada do vetor no ponto , ou seja:
Aplicando o ponto :
Juntando tudo, a gente tem a nossa figura no gráfico.
Valeu, galera! Até a próxima! 😉