![]()
Passo 1
Vamos começar pelas curvas de nível.
Sempre que falamos sobre curva de nível, o que temos que fazer é igualar nossa função a uma constante qualquer.
Assim, as curvas de nível da nossa função são
Que diabo é isso?
Parece complicado, mas na real, o é um valor constante, o 1 é uma constante, logo, o que temos é
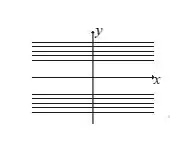
Ou seja, linhas retas, com valores constantes em , acima e abaixo da origem, por conta do sinal de + e -.
Ah, a gente tem que só que ficar atento que, como o tá no denominador, quanto maior for o valor de , menor será o valor de , beleza? Então, valores de mais perto da origem correspondem a valores de maiores.
Temos isso aqui:
Passo 2
Beleza, agora que já temos as curvas de nível, precisamos identificar o gráfico da nossa função. Mas, dessa vez, parece mais fácil identificar o gráfico 3D a partir da expressão da função mesmo, sem se ligar nas curvas de nível.
Nossa função é
Se isso fosse algo em 2D, teríamos uma hipérbole assim:
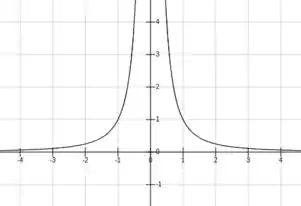
Certo?!
O eixo horizontal é o eixo e o vertical é o eixo .
Então, em 3D o que teremos é um cilindro cuja geratriz é essa hipérbole, assim:
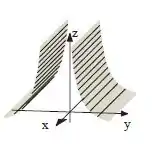
Resposta
