UFF, Cálculo 2B, Listas GMA, Lista 1, questão 5.
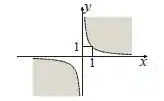
Descreva e esboce o maior domínio possível da função real de duas variáveis, isto é, descreva analiticamente e represente geometricamente o maior subconjunto do que torna a expressão que define a função verdadeira em .
Passo 1
Lembra do gráfico da função logarítmica?
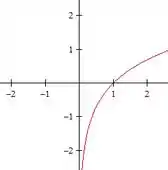
Aqui a gente pode perceber que o domínio do é tal que seu argumento tem que ser sempre maior do que zero. Assim
Passo 2
Agora, se fizermos
Temos a hipérbole
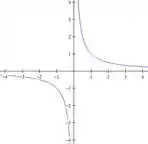
Como no nosso domínio temos o sinal de maior “”, significa que o desenho do nosso domínio é a região que está acima do gráfico da hipérbole.
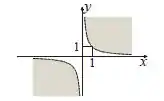
Resposta
Exercícios de Livros Relacionados
Seja g x , y = c o s ( x + 2 y ) .Calcule g ( 2 , - 1 ) .Determine o domínio de g . Determine a imagem de g
Seja f x , y , z = x + y + z + ln ( 4 - x 2 - y 2 - z 2 ) .Calcule f ( 1,1 , 1 ) .Determine o domínio de f .
Seja f x , y =x 2 e 3 x y .(a) Calcule f 2,0 .(b) Determine o domínio de f .(c) Determine a imagem de f .
As alturas de onda h em mar aberto dependem da velocidade v do vento e do tempo t que o vento tem soprado a essa velocidade. Os valores da função h = f v , t , td estão registrados nos pés na Tabela 4
1. Desenhe a imagem:c)F (t) = (t , t , 1) , t = 0