UFF, Cálculo 2B, Listas GMA, Lista 1, questão 15.
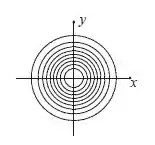
Esboce as curvas de nível e o gráfico da função
Passo 1
Para achar as curvas de nível da função, fazemos
Ou seja, temos circunferências centradas na origem e raio igual a
Passo 2
Beleza, mas não podemos ter raiz de número negativo né?
Então temos que ver para que valores de , .
Do gráfico da função logarítmica
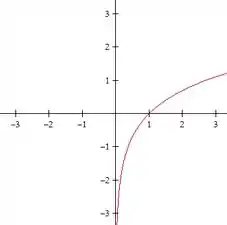
Vemos que
Passo 3
Agora o que temos que fazer é variar os valores de , ou seja, variar o raio do círculo.
Se , temos
Se , temos
Se , temos
Ou seja, a medida que fazemos ficar cada vez menor que 1 (mas ainda sempre maior que zero), o raio do nosso circulo vai ficando maior.
Dessa forma, nossas curvas de nível são vários círculos concêntricos, que vão ficando cada vez maiores, conforme diminuímos o valor de .
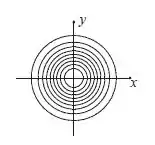
E assim, como quanto maior (mais alto) o nosso plano estiver, menor será nosso raio, nosso gráfico será:
Resposta
