![]()
![]()
Passo 1
Vamos começar pelas curvas de nível.
Sempre que falamos sobre curva de nível, o que temos que fazer é igualar nossa função a uma constante qualquer.
Assim, as curvas de nível da nossa função são
Beleza, isso soa parecido com algo que a gente já viu antes na vida.
Imagina que esse . Nesse caso, teremos a função
Que sabemos que tem um gráfico com essa cara aqui:
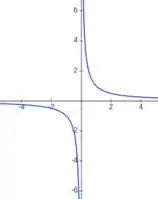
Mas, em vez de termos um 1, a gente tem um valor qualquer , que pode ser positivo ou negativo.
Beleza, mas o que que acontece quando a gente fizer o aumentar positivamente ou então diminuir negativamente?
No caso de usarmos valores positivos para e maiores do que 1, o que acontece é que nosso gráfico vai se “afastando” dos eixos. Já se usarmos valores negativos de , teremos o mesmo gráfico, que se comportará da mesma forma, só que desenhado no segundo e no quarto quadrante.
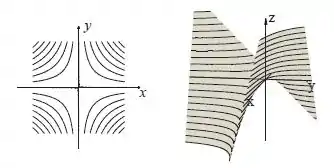
Assim, nossas curvas de nível terão essa cara aqui:
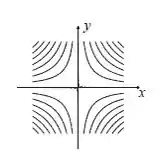
Passo 2
Beleza, agora que já temos as curvas de nível, precisamos identificar o gráfico da nossa função. E vamos fazer isso a partir das próprias curvas de nível.
Pensa comigo e tenta imaginar essas curvas saindo do plano e “subindo” para o espaço. Vai formar uma figura toda esquisitona, bem parecida com um parabolóide hiperbólico.
Vamos então ter isso aqui:
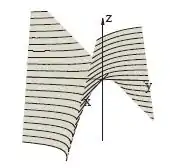
Muito estranho isso né?! Vamos torcer pra não cair assim na prova.
Mas se cair também, você já vai saber fazer, não vai?! Afinal, a gente acabou de fazer juntos aqui treinando pra sua prova!!
Fé no pai que o diploma sai. Vamo que vamo.
Resposta