![]()
Passo 1
Vamos lá, temos a função arcoseno, que olhando assim de cara, a gente pode não se lembrar qual a restrição de domínio pra essa bagaça.
Mas aí, pensa comigo, a gente sabe que a função arcoseno é a função inversa da função seno. E a gente sabe também que o domínio da função inversa é a mesma coisa que a imagem da função normal...
E imagem da função seno a gente sabe de cor e salteado, pois a gente sabe que a função seno só assume valores de -1 até 1.
Isso significa então, que a restrição de domínio pra nossa função são valores de -1 até 1. Ou seja, o que tá dentro da nossa função arcoseno tem que estar dentro desse intervalo. Assim
Passando o sinal de menos para os dois lados, a gente inverte o sinal e fica com
Como a gente pode só reorganizar isso assim:
E esse é nosso domínio :)
Passo 2
Pra desenhar isso agora, vamos pensar nessas duas (des)igualdades separadamente:
e
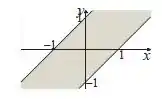
Se fossem igualdades, essas coisas seriam duas retas paralelas. Como são desigualdades, a gente pode pensar nessas retas como algo que define um espaço entre elas, incluindo a borda desse espaço, que são as retas propriamente ditas (por causa do sinal de igual também).
Parece confuso escrevendo, mas olha só como é o desenho:
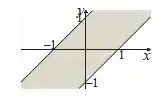
Resposta
![]()