Na figura temos, respectivamente, o desenho das curvas de nível das seis funções a seguir.
Faça a associação destas seis curvas de nível com cada um dos seis gráficos apresentados na figura
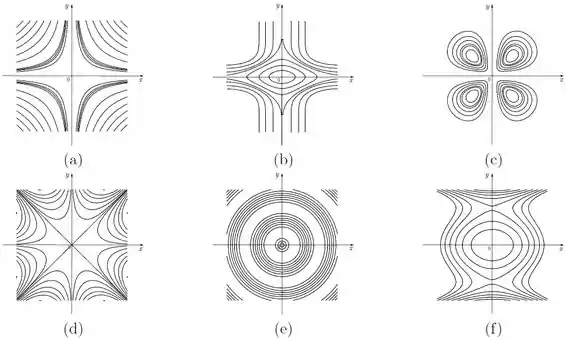
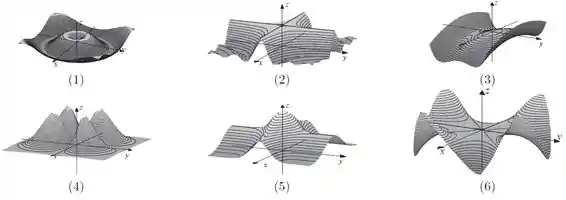
Passo 1
Calma, não é tão difícil quanto parece. Ele não pediu para você terminar as curvas de nível ele de deu algumas curvas de nível e quer a função. Ignora a fórmula de cada função, fica ligado só na curva de nível.
Passo 2
Olha para essas curvas de nível, primeiro detalhe é que a curva é simétrica nos dois eixos, isso diminui nossas possibilidades. Depois repara que as curvas são ondas que vão se separando as poucos, consegue perceber que a função que tem essas curvas de nível é a função ?
Você tem ondas se afastando e meio que subindo sacou? Vamos para a próxima.
Passo 3
Dessa vez as curvas de nível começam em uma “bolinha” distorcidas e vão distorcendo cada vez mais de forma parecida ao longo dos eixos, nas 4 direções, repara que não é igual mas é bem parecido. A única dessa forma é a função
Passo 4
Essa é mais de boa, qual das funções tem círculos que vão se deformando um pouquinho? É a função
Passo 5
Essa é a única função que tem uma curva de nível que faz um passando por cima da origem? Só temos a função fazendo isso.
Passo 6
Essa são circunferências que estão um pouco agrupadas, depois tem um espaço vazio, depois agrupa de novo, só temos a função fazendo isso.
Passo 7
Bem essa é a mais fácil de todas, é a que sobrou né? Rs. Então sua função vai ser .