UFF, Cálculo 2B, Listas GMA, Lista 1, questão 9c.
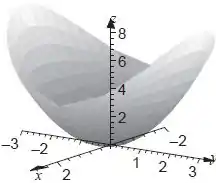
Considere a função de duas variáveis
Definida em um subconjunto de . Faça um esboço do gráfico de para o caso abaixo
Passo 1
Para fazer o gráfico dessa função devemos primeiro entender como é a função .
Repara que temos
Isso parece muito a equação de uma circunferência, onde o raio vai ser então vamos ter várias circunferências com seus raios mudando.
Se olharmos o gráfico por cima vamos ver muitas circunferências com o raio variando, onde o raio vai ser e a posição da altura dele vai ser
O primeiro raio vai ser com e vai ser a própria origem, depois o raio vai aumentando com , o seu gráfico sem a restrição vai ficar
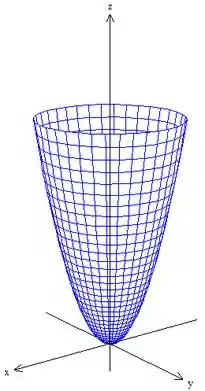
Passo 2
Vamos entender agora como aquele domínio vai mudar o gráfico da função.
Repara que ele quer uma limitação que é um disco elíptico.
Ou seja, ele está limitando toda e qualquer curva de nível de a essa elipse.
Mas cada curva de nível é um circulo certo? Vão aparecer pontas na parte de cima do gráfico, isso porque vamos pegar algumas partes de circunferências mas não ela toda. Olhando de cima, pensando sem a restrição vamos ter algo assim
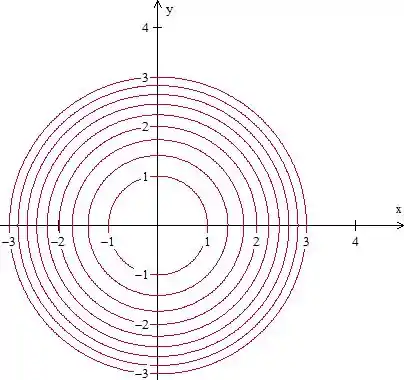
Com a limitação vai ficar assim
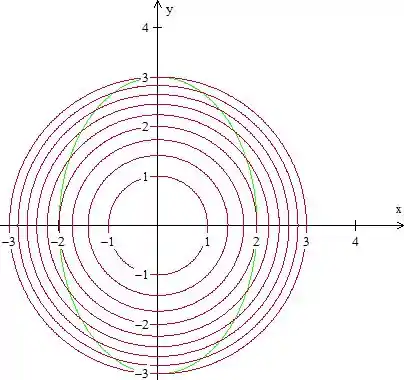
Assim vamos ter algumas partes de circunferências em vez da circunferência completa.
O gráfico vai ficar
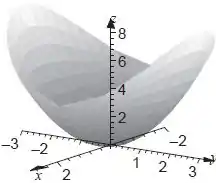
Resposta
