Mas, antes de saber os valores de , vamos descrever direitinho qual é o conjunto de nível da nossa função .

Para isso, precisamos saber o domínio da nossa função, porque se a função não estiver definida em algum ponto, também não dá pra ter conjunto de nível nesse ponto, ne?!

Tá, observando nossa função

Vamos que ela tem a restrição do denominador. Então

Assim

Beleza, mas ainda precisamos saber quais são os possíveis valores que pode assumir, pra poder fazer ele variar nesses valores e, assim, obtermos todos os conjuntos de nível da nossa função.

Vamos começar determinando todos os valores que pode assumir pra podermos encontrar nossos conjuntos de nível.

Temos

Isso não tem restrição nenhuma, né? Então significa que nosso pode assumir qualquer valor.

Então

Agora vamos fazer o variar dentro desse intervalo para saber todos os conjuntos de nível da nossa função.

Nosso conjunto de nível é

E isso nada mais é do que a equação de uma reta.

Fazendo o variar para , e , o que acontece é que a gente estará mudando a inclinação da nossa reta.

Maaaaas, antes de sair indo pra representação geométrica dos nossos conjuntos de nível (as tais das retas), a gente tem que lembrar que nossa função não tá definida em , o que significa que nossas retas NÃO podem passar por esse ponto, beleza?

Então quando a gente tiver desenhando, em a gente tem que “fazer um furo” na reta.

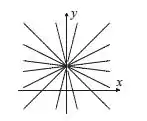
Então, a representação geométrica de todos os conjuntos de nível que podemos ter fica assim