UFF, Cálculo 2B, Listas GMA, Lista 1, questão 4.
Descreva e esboce o maior domínio possível da função real de duas variáveis, isto é, descreva analiticamente e represente geometricamente o maior subconjunto do que torna a expressão que define a função verdadeira em .
Passo 1
Opa, aqui nossa única restrição é que temos uma raiz quadrada. Assim, o que está dentro dela tem que ser sempre maior ou igual a zero. Então
Ao mesmo tempo,
Porque são duas coisas somadas, elevadas ao quadrado.
Passo 2
Dessa forma, temos o disco de raio 1. O desenho fica
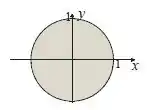
Resposta
Exercícios de Livros Relacionados
Seja g x , y = c o s ( x + 2 y ) .Calcule g ( 2 , - 1 ) .Determine o domínio de g . Determine a imagem de g
Seja f x , y , z = x + y + z + ln ( 4 - x 2 - y 2 - z 2 ) .Calcule f ( 1,1 , 1 ) .Determine o domínio de f .
Seja f x , y =x 2 e 3 x y .(a) Calcule f 2,0 .(b) Determine o domínio de f .(c) Determine a imagem de f .
As alturas de onda h em mar aberto dependem da velocidade v do vento e do tempo t que o vento tem soprado a essa velocidade. Os valores da função h = f v , t , td estão registrados nos pés na Tabela 4
1. Desenhe a imagem:c)F (t) = (t , t , 1) , t = 0