UFF, Cálculo 2B, Listas GMA, Lista 1, questão 36.
Resolva as questões abaixo:
- Faça o gráfico da função . Escreva uma função cuja curva de nível associado ao nível 0 é igual ao gráfico de .
- Mais geralmente, dada uma função , escreva uma função cuja curva de nível associada ao nível 0 é igual ao gráfico de . O que você pode dizer a respeito das curvas de nível de para níveis diferentes de 0?
- Seja z. Escreva uma função cuja superfície de nível associado ao nível 0 é igual ao gráfico de .
- Mais geralmente, dada uma função , escreva uma função cuja superfície de nível associada ao nível 0 é igual ao gráfico de . O que você pode dizer a respeito das curvas de nível de para níveis diferentes de 0?
Passo 1
Bom, isso é uma função de uma variável. Então, podemos desenhar essa parábola tranquilamente, como sabemos desde o ensino médio.
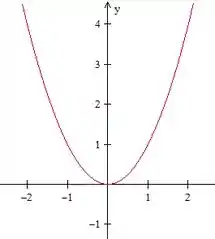
Agora precisamos escrever uma função de duas variáveis, que quando a igualarmos a zero (para achar a curva de nível zero), cheguemos na mesma expressão que essa equação de uma variável que acabamos de desenhar. Podemos fazer assim então:
Assim, quando fizermos teremos
Que é exatamente a nossa função de uma variável.
Passo 2
Assim, podemos concluir que se temos uma função de uma variável, para transformarmos numa função de duas variáveis que terá a curva de nível zero igual ao gráfico de , basta fazermos:
Se igualamos isso a zero, voltamos exatamente para a expressão de .
Se igualarmos isso a outros níveis diferentes de zero, teremos
Que nada mais é do que o gráfico de deslocado para cima (se ) ou para baixo (se ).
Passo 3
Analogamente ao que a gente fez na letra a, vamos acrescentar a variável e fazer:
Porque assim, quando igualarmos isso ao nível zero, voltaremos para a expressão da nossa função de duas variáveis.
Passo 4
Do mesmo modo, podemos concluir que se temos uma função de duas variável, para transformarmos numa função de três variáveis que terá a curva de nível zero igual ao gráfico de , basta fazermos:
Se igualamos isso a zero, voltamos exatamente para a expressão de .
Se igualarmos isso a outros níveis diferentes de zero, teremos
Que nada mais é do que o gráfico de deslocado para cima (se ) ou para baixo (se ).
Resposta
Ei, a resposta está no passo a passo :)