USP, Sem Campus, Física 1, Coletânea de Exercícios - Parte I - Cinemática, Leis de Newton, Trabalho e e Energia, Questão 47a
Um bloco desliza, para baixo, sobre um plano de inclinação , com velocidade constante. Ao atingir o final do plano, ele é projetado plano acima, por um dispositivo, com velocidade inicial . A aceleração da gravidade é .
Que distância acima, no plano, ele percorrerá, antes de parar?
Passo 1
Eaew, tudo bem com você?
A situação acima é bastante peculiar! Note que ele desce em um plano inclinado que tem como inclinação o ângulo , até aí tudo bem! Mas… ele desce com velocidade constante! Isso só é possível se houver alguma força contrário (atrito) que iguala a componente do peso que acelera o bloco abaixo! Mas, por que isso é importante neste caso? Nesta situação o esquema será
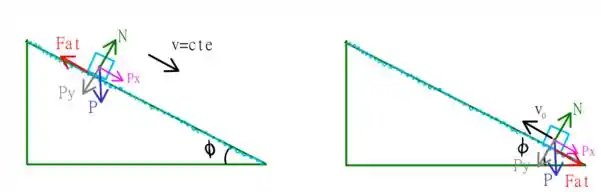
Note que ao subir essa força de atrito também influencia o movimento! Portanto a aceleração que faz o corpo parar é composta pela componente peso mais um termo devido a força de atrito! Vamos primeiro estimar a nossa força de atrito, e depois verificar a altura que o corpo alcançará! Bora lá!
Passo 2
Primeiro, se a velocidade é constante, temos que a aceleração que faria o corpo acelerar plano abaixo é nula, de forma que
em que considerei apenas a componente do peso que está na direção do movimento! Note que não precisamos saber nada além disso, já que estamos lidando com um ângulo arbitrário! Vamos analisar o caminho de volta!
Passo 3
Na volta, temos agora que o atrito ajuda a componente da força peso, de forma que
usando o resultado do passo anterior, temos que
ou simplesmente
Note que a força não precisava ser uma força de atrito! Poderia ser qualquer força, estou usando atrito simplesmente pois é o mais comum neste tipo de problema! Agora, que equação relaciona aceleração, velocidade e deslocamento?
Passo 4
A equação de Torricelli é o caminho, temos que
escolhi o sinal negativo já que o sistema está desacelerando. Como queremos analisar a situação quando o corpo parar, temos que , de forma que o deslocamento ao longo do plano , é dado por
Usando a aceleração que obtivemos no passo anterior temos que
Esse é o deslocamento ao longo do plano que procurávamos! Essa alternativa foi isso! Vamos para a pr��xima!