UFRJ, Sem Campus, Física 1, Listas de F1 - Engenharias UFRJ Macaé - 3ª Lista - Dinâmica - Leis de Newton, Questão 3a
Um bloco de está sobre uma cunha sem atrito que tem uma inclinação de e uma aceleração para a direita, de tal forma que a massa permanece estacionária em relação a cunha (cf. figura).
(a) Desenhe o diagrama de corpo livre do bloco e use-o para determinar a magnitude da aceleração.
Passo 1
Eaee!!! Belezinha? Bom... a questão nos dá o seguinte sistema envolvendo um bloco de e um plano inclinado:
Nesse sentido, a questão nos pede para desenharmos o diagrama de corpo livre e, com ele, devemos calcular a nossa aceleração .
E aí? Bora lá?
😉
Passo 2
Então... Para isso, devemos lembrar que o ângulo de apresentado é o mesmo entre o bloco e a horizontal.
Ademais, a força gravitacional do bloco sempre aponta para baixo e a força normal é sempre perpendicular ao plano em que o bloco está situado.
Assim, temos o nosso diagrama de corpo livre:
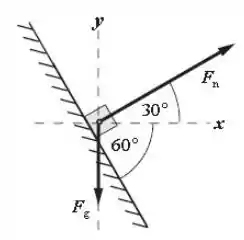
Passo 3
Assim, aplicando a Lei de Newton, temos:
Decompondo na vertical, temos:
Como o corpo está estacionário, então , logo:
Passo 4
Por outro lado, decompondo no eixo :
Assim, dividindo as duas equações, temos:
Entendeu direitinho? Responde aee ;)
