Um corpo de massa é visto descendo um plano com velocidade constante; só há o plano e o corpo. Sabendo-se que o ângulo de inclinação do plano em relação à horizontal é igual a , pode-se afirmar que a resultante das forças que o plano inclinado exerce sobre o corpo tem módulo igual a
Passo 1
Vamos começar vendo as forças que atuam nesse corpo.
Vamos responder as perguntas do passo a passo para colocar as forças
- A massa dele é considerada?
- Ela esta encostada em alguma superfície?
- Tem algum fio?
- Tem mola?
- Tem atrito?
Sim, ele tem massa.
Sim, o bloco está em contato com o chão.
Não, não existe um fio atuando.
Não, não existe mola atuando.
Sim, existe atrito.
Se o bloco desliza pelo plano com velocidade constante, quer dizer que existe alguma força que o chão exerce em oposição a força da gravidade, essa força chamamos de força de atrito, afinal se a força da gravidade atuasse sozinha no sistema, o bloco iria deslizar acelerando pela rampa, com velocidade crescente.
A força de atrito é quem impede o bloco de acelerar, fazendo ele se movimentar com velocidade constante.
O movimento do boloco é para direita logo a força de atrito é para a esquerda no . O DCL do bloco fica
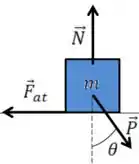
Já vimos que quando temos um plano inclinado, é mais fácil considerarmos a horizontal e vertical em relação a superfície inclinada, isso facilita nossas contas porque ele não tem movimento vertical em relação a essa superfície.
O ângulo fica na força peso com a vertical quando fazemos isso.
Passo 2
Repare que ele quer a força que é a resultante do chão, o que isso quer dizer?
Como o bloco está em movimento uniforme, a sua aceleração é nula e a força resultante sobre ele é nula. Usando essa informação podemos achar e .
Repare que, no
Enquanto, no
Isso nós diz que as componentes da força resultante do chão são as mesmas componentes da força peso, então
Resposta
Letra B