Um bloco desliza, para baixo, sobre um plano de inclinação , com velocidade constante. Ao atingir o final do plano, ele é projetado plano acima, por um dispositivo, com velocidade inicial . A aceleração da gravidade é .
Ele tornará a deslizar para baixo no plano inclinado? Explique.
Passo 1
Eaew, tudo bem com você?
A situação acima é bastante peculiar! Note que ele desce em um plano inclinado que tem como inclinação o ângulo , até aí tudo bem! Mas… ele desce com velocidade constante! Isso só é possível se houver alguma força contrário (atrito) que iguala a componente do peso que acelera o bloco abaixo! Mas, por que isso é importante neste caso? Nesta situação o esquema será
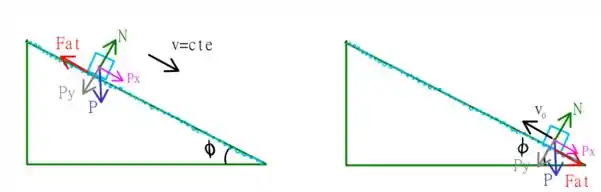
Na alternativa anterior obtivemos que o corpo sobe ao longo do plano a distância
e, então para. Essa alternativa pede para analisarmos se o corpo voltará a descer! Vamos analisar a situação!
Passo 2
Note que estou considerando que a força que mantém o corpo descendo em velocidade constante é a força de atrito. Se for uma força arbitrária, temos que não há razão para o corpo não voltar a descer! Já que são as propriedades do atrito estático e cinético que fazem surgir esta propriedade! Então, se a força for realmente atrito, qual será a situação? Existem dois tipos de atrito a se considerar agora! A força de atrito cinética, que nesta situação tem módulo dada por
ou seja, temos que o coeficiente de atrito cinético é dado por
O atrito estático no entanto deve obedecer a seguinte desigualdade
em que a igualdade indica a situação em que o atrito é mais intenso!
Passo 3
Temos que ao parar no plano, a força de atrito será necessariamente
O corpo ficará parado se o atrito for igual à
portanto, temos a relação
usando a relação que obtivemos anteriormente para o coeficiente de atrito cinético, temos que
Em geral, temos que , portanto, temos que o corpo não voltará a descer! A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
O corpo não voltará a descer!