Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Plano Inclinado

Ver Teoria
Exercício 671234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666869707172737475

Enunciado

UFV, Sem Campus, Física 1, P2 - 2021.2, Questão 1

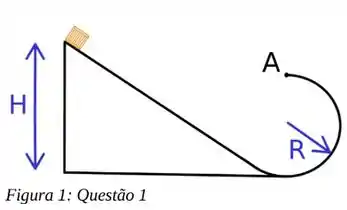
Uma caixa está em repouso no alto de uma rampa inclinada de altura H. No final da rampa é posicionado um arco de circunferência de raio R, como ilustrado na figura abaixo. Em termos do raio R, qual a menor altura H para que a caixa atinja o ponto mais alto da circunferência (ponto A)? Desconsidere qualquer tipo de atrito

Passo 1

Fala galera, bora resolver nosso exercício?

Bom, antes de começar, vamos entender aqui o que faremos. Para começar, nossa caixa vai partir do repousou de uma certa altura H, vai chegar no final da nossa rampa e vai dar um looping na nossa circunferência. O que queremos saber aqui é a altura mínima para que a nossa caixa consiga passar no ponto A na iminência de soltar da circunferência. Ok?

Para isso, vamos precisar dos conceitos de Força Centrípeta:

F = m v 2 R

E também da Conservação da Energia Mecânica:

E M i = E M f

Passo 2

Vamos começar analisando a nossa circunferência:

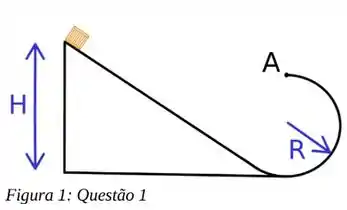
Reparem que como queremos a força centrípeta da nossa caixa no Ponto A, nós vamos ter uma velocidade que é tangente a nossa circunferência e teremos a forças que apontam para o centro da circunferência e para baixo.

F = m v 2 R

No caso, essas forças serão a Peso e a Normal. Como elas duas apontam para a mesma direção, podemos dizer que:

P + F = m v 2 R

Show? Mas lembra que queremos a altura mínima ne? Para isso, nossa caixa tem que estar na iminência de sair da circunferência, logo, podemos desconsiderar a força Normal:

P = m v 2 R

Sabendo que P = m g :

m g = m v 2 R

R g = v 2

Ok, vamos deixar como está que logo usaremos.

Passo 3

Ok, agora vamos trabalhar a conservação da Energia Mecânica:

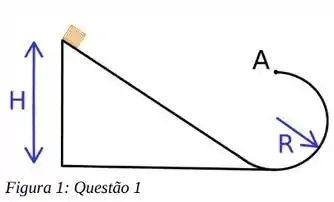
Na nossa fórmula, usaremos:

E M i = E M f

K i + U i = K f + U f

Vamos lá. No início da nossa rampa, a nossa caixa parte do repouso, logo a velocidade dela é zero. Com isso, a energia cinética inicial é zero.

U i = K f + U f

m g H = m v 2 2 + m g h

No caso, a nossa velocidade ali vai ser a velocidade que a caixa tem no Ponto A. Sabe aquele h que temos ali também? Essa altura vai ser do Ponto A até o chão, que é justamente o diâmetro da circunferência:

m g H = m v 2 2 + m g 2 R

Além disso, lembra da velocidade que achamos no Passo 2? Vamos usar aqui

m g H = m R g 2 + m g 2 R

Reparem que podemos simplificar m g dos dois lados:

H = R 2 + 2 R

H = 5 R 2

Resposta

H = 5 R 2

Exercícios de Livros Relacionados

A Fig. 5-56 mostra uma caixa de massa m 2 = 1,0k g sobre um plano inclinado sem atrito de ângulo θ = 30 ° . Ela está ligada por uma corda de massa desprezível a uma caixa de massa m 1 = 3,0k g sobre u
Dois blocos, cada um com peso p , são mantidos em equilíbrio em um plano inclinado sem atrito (Figura 5.48 ). Em termos de p e do ângulo a do plano inclinado, determine a tensão: a) na corda que conec
Um fio horizontal segura uma bola sólida e uniforme de massa m sobre uma rampa inclinada, que forma um ângulo de 35 ° acima do plano horizontal. A superfície dessa rampa é perfeitamente lisa, e o fio
Bagagens são transportadas de um local a um outro de um aeroporto por uma esteira. Em um certo local a esteira tem uma inclinação de 2,5 ° com a horizontal. Suponha que para ângulo tão pequeno as mala
Um bloco começa a subir um plano inclinado sem atrito com uma velocidade inicial v 0 = 3,50m / s . O ângulo do plano inclinado é θ = 32,0 ° . (a) Que distância ao longo do plano inclinado o bloco cons