Força e Leis de Newton
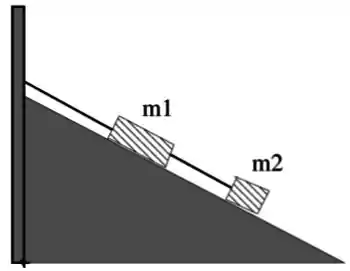
Dois blocos de massas e estão ligados por uma corda em um plano inclinado sem atrito que forma um ângulo de em relação a horizontal, conforme figura. Se a corda que liga os blocos se rompe, calcule o módulo da aceleração do bloco .
a)
b)
c)
d)
e) nenhuma das anteriores
Passo 1
Após romper a corda, o bloco de massa terá apenas a força peso atuando sobre ele.
Decompondo a força peso na horizontal e vertical, temos que na vertical a componente vertical da força peso se anulará com a força normal, já que o bloco não possui movimento na vertical. E a componente horizontal irá acelerar o bloco.
A decomposição fica:
Utilizando a segunda lei de Newton temos:
Cortando as massas temos:
Adotando :
Resposta
Alternativa .
Exercícios de Livros Relacionados
A Fig. 5-56 mostra uma caixa de massa m 2 = 1,0k g sobre um plano inclinado sem atrito de ângulo θ = 30 ° . Ela está ligada por uma corda de massa desprezível a uma caixa de massa m 1 = 3,0k g sobre u
Dois blocos, cada um com peso p , são mantidos em equilíbrio em um plano inclinado sem atrito (Figura 5.48 ). Em termos de p e do ângulo a do plano inclinado, determine a tensão: a) na corda que conec
Um fio horizontal segura uma bola sólida e uniforme de massa m sobre uma rampa inclinada, que forma um ângulo de 35 ° acima do plano horizontal. A superfície dessa rampa é perfeitamente lisa, e o fio
Bagagens são transportadas de um local a um outro de um aeroporto por uma esteira. Em um certo local a esteira tem uma inclinação de 2,5 ° com a horizontal. Suponha que para ângulo tão pequeno as mala
Um bloco começa a subir um plano inclinado sem atrito com uma velocidade inicial v 0 = 3,50m / s . O ângulo do plano inclinado é θ = 32,0 ° . (a) Que distância ao longo do plano inclinado o bloco cons