USP, Sem Campus, Física 1, Coletâneas de Exercícios - Parte I - Cinemática, Leis de Newton, Trabalho e Energia, Questão 36a
36. Um bloco de está parado sobre um plano inclinado, devido ao atrito. Qual a componente da força que aplica no plano inclinado:
(a) Perpendicular à superfície e tangente à superfície?
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉
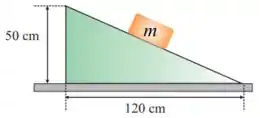
Nesse problema temos um bloco de massa que está apoiado em um plano inclinado e devido ao atrito, ele se encontra em repouso.
Com essas informações, queremos descobrir qual é a força que o bloco aplica na superfície inclinada perpendicularmente e tangencialmente.
E aí, como vamos fazer isso? 🤔
Pra resolver esse problema, temos que ter em mente qual é a força que o bloco aplica na superfície e com isso encontrar uma maneira de decompor essa força em duas componentes, uma perpendicular e outra tangencial à superfície.
Entendeu? Bora lá! 😉
Passo 2
Como o bloco está em repouso, ele não possui aceleração, logo, as únicas forças que atuam sobre ele é a força de atrito (que mantem o bloco em repouso) e a força peso (devido a ação da gravidade).
A princípio, podemos ignorar a força de atrito e olhar apenas para a força peso
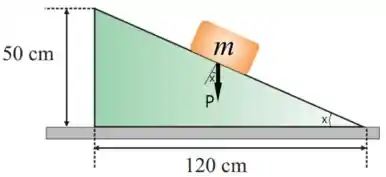
Podemos definir um ângulo que o plano faz com a horizontal e fazendo algumas relações angulares, podemos afirmar que o ângulo que a força faz com eixo perpendicular à superfície também é .
Assim, podemos decompor em relação ao plano inclinado que pela lei dos cossenos e dos senos, temos
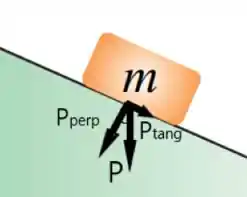
Tranquilo até aqui? 👀
Passo 3
Sabemos que a força é dada por
Já o ângulo pode ser obtido a partir da equação da tangente
Substituindo e nas componentes da força peso, vamos obter
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍
