UFSCAR, Sorocaba, Física 1, Listas de Física 1 - UFSCAR (Sorocaba) - Lista 3, Questão 8
Um bloco de massa está sobre um plano inclinado de um ângulo com a horizontal. O coeficiente de atrito cinético entre o bloco e o plano é . O bloco está amarrado a um segundo bloco de massa que pende livremente de um cordão que passa por uma polia sem massa e sem atrito. Depois que o segundo bloco caiu , qual sua velocidade?
Passo 1
Eaee!!! Belezinha? Bom... a questão nos dá um sistema de dois blocos de acordo com a seguinte figura:
Desejamos descobrir a velocidade do bloco quando o bloco cai .
Como a questão não nos deu intervalo de tempo, podemos utilizar a equação de Torricelli:
Onde é a velocidade final, é a velocidade inicial, é a aceleração e é a distância percorrida.
Mas antes disso, devemos verificar o diagrama de corpo livre de cada bloco e aplicar a Segunda Lei de Newton, que é dada por:
Onde é a força e é a massa.
Não entendeu? Então bora junto 😉
Passo 2
Bom... fazendo o diagrama de corpo livre para os dois casos, temos:
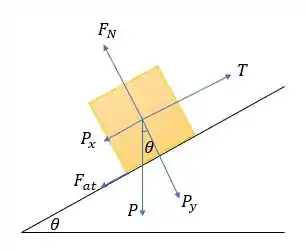
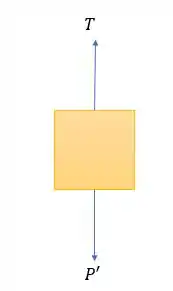
Onde:
- é a força normal;
- é o peso;
- é a força de atrito;
- é a tração da corda;
- e são as componentes de .
Passo 3
Pelo diagrama de corpo livre do bloco da primeira imagem e a Segunda Lei de Newton, podemos determinar a aceleração do sistema:
Como , temos:
Por outro lado, pelo diagrama de corpo livre do bloco da segunda imagem, temos:
Substituindo , temos:
Passo 4
Dessa forma, quando o segundo bloco cai com aceleração de partindo do repouso, ele adquire a seguinte velocidade:
Entendeu direitinho? Responde aee ;)
