9) Um alpinista de massa que visa agilizar a sua subida por uma parede vertical de uma encosta triangular se utiliza da liberação e deslizamento de uma caixa de equipamentos de massa pelo lado inclinado em da encosta e uma corda de massa desprezível. Ele se dependura na extremidade livre da corda cuja outra extremidade está amarrada à caixa e se solta. Sabe-se que o coeficiente de atrito cinético entre a caixa e a superfície da encosta é e a presença de uma polia no alto da encosta permite a livre movimentação da corda.
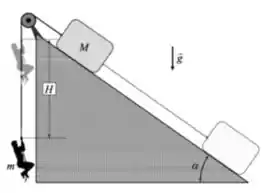
- Faça um diagrama mostrando todas as forças que atuam tanto na caixa quanto no alpinista quando eles estiverem em movimento.
- Escreva a segunda lei de Newton para a caixa e para o alpinista.
- Obtenha os módulos das acelerações e da caixa e do alpinista respectivamente bem como os módulos das forças de tensão e na corda em cada um dos lados da encosta.
- Determine o intervalo de tempo que levará para que o alpinista suba uma altura supondo que ele pariu do repouso e que , e
Dados: e .
Passo 1
Fala aí, galerinha!!
Esse problema é um problema típico de dinâmica. A gente vai ter que fazer um roteirinho e aplicar as leis de Newton. O problema nos fala sobre um alpinista que está preso em uma corda e na outra extremidade da corda tem uma caixa de equipamentos tão pesada que desliza e faz com que o alpinista suba.A parte boa é que o roteiro para resolver essa questão já está na ordem dos itens que o problema nos dá. Então vamos lá.... A primeira coisa que a gente tem que fazer quando nos deparamos com esse tipo de problema é marcas as forças que atuam nos corpos que estamos interessados. Nesse caso temos o alpinista e a caixa. a) As forças que atuam no alpinista são a força peso e a tração da corda , então temos:

Para a caixa, temos 4 forças atuam: O peso da caixa (sempre apontando para o centro da terra), a normal da superfície (sempre perpendicular à superfície), a tração da corda e a força de atrito (como a caixa está deslizando para baixo, ela aponta contrário à este deslize). Então temos:
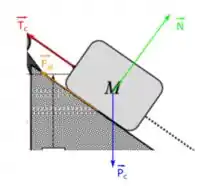
Passo 2
b) Agora a gente tem que escrever a segunda lei de Newton para cada um dos corpos. Vamos começar com o alpinista. A segunda lei de Newton nos fala que a soma vetorial de todas as forças que atuam sobre o alpinista de massa é:
Como as forças que atuam no alpinista só estão no eixo vertical e adotando o sentido para cima como o positivo, temos então:
Como :
Ou seja, temos:
Passo 3
Da mesma maneira, para a caixa, temos:
Agora, como estamos em um plano inclinado temos que escrever essas equações para cada componente. A gente faz isso adotando um plano cartesiano alinhado com o plano inclinado. Então a gente faz um diagrama do corpo livre para a caixa como esse aqui:
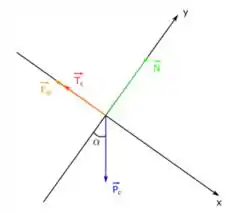
Por esse diagrama, percebemos que a única força que precisamos decompor é o peso da caixa . Nele a gente percebe que temos uma componente no sentido negativo de e uma no sentido positivo de então escrevemos:
A componente em como está com o ângulo é
E a componente como está sem o ângulo é:
Então o peso fica escrito como:
Como , temos:
Então a segunda lei de Newton para a caixa, em termos das componentes é:
Ou, isolando as componentes temos as equações:
Passo 4
c) Para encontrarmos as acelerações, vamos ter que resolver o sistema formado pelas equações que a gente obteve quando escrevemos a segunda lei de Newton para os corpos:
Antes de tentarmos, vamos melhorar essas equações pensando que o fio e a polia são ideias. Dessa maneira, teremos a mesma tração em qualquer ponto do fio e a aceleração do sistema vai ser a mesma. Ou seja:
As nossas equações ficam:
A última equação nos dá:
Como temos que as duas primeiras equações se tornam:
Somando essas duas equações temos:
Arrumando um pouco temos:
Se levarmos esse resultado na primeira equação do nosso sistema e isolarmos o temos:
Passo 5
d) Agora o exercício nos dá alguns valores e pede que a gente encontre o intervalo de tempo que levará para que o alpinista suba uma altura . Beleza! Se agora a gente sabe que o alpinista sobe com aceleração constante dada por , que substituindo os valores temos:
A gente pode a equação horária para o alpinista que sobre em um MRUV:
Adotando que o alpinista sai da origem com velocidade inicial nula temos:
Então
Resolvemos essa 😊 Vamos para a próxima??
Resposta
Ei, a resposta está no passo a passo :)