Dois blocos ligados entre si por uma corda estão pendurados em um plano inclinado, de acordo com a figura abaixo. Não há atrito entre os blocos e o plano inclinado. A tensão medida na corda que liga o bloco de massa à parede é três vezes maior que a tensão que liga o bloco ao bloco . É correto afirmar que a razão entre as massas vale:
a)
b)
c)
d)
e)
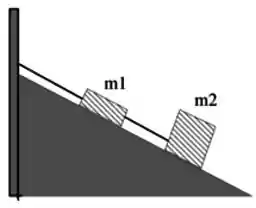
Passo 1
Considerando o ângulo mostrado na figura e as forças atuando em cada bloco:
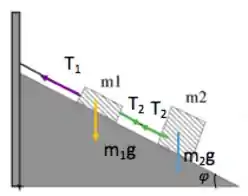
Escrevendo a equação pra cada bloco:
Mas sabemos que a aceleração é zero, certo? Então:
Sabemos também que . Dividindo uma equação pela outra:
Cortando esse seno e essa gravidade, fica assim:
Chegamos finalmente em:
Resposta
b)
Exercícios de Livros Relacionados
A Fig. 5-56 mostra uma caixa de massa m 2 = 1,0k g sobre um plano inclinado sem atrito de ângulo θ = 30 ° . Ela está ligada por uma corda de massa desprezível a uma caixa de massa m 1 = 3,0k g sobre u
Dois blocos, cada um com peso p , são mantidos em equilíbrio em um plano inclinado sem atrito (Figura 5.48 ). Em termos de p e do ângulo a do plano inclinado, determine a tensão: a) na corda que conec
Um fio horizontal segura uma bola sólida e uniforme de massa m sobre uma rampa inclinada, que forma um ângulo de 35 ° acima do plano horizontal. A superfície dessa rampa é perfeitamente lisa, e o fio
Bagagens são transportadas de um local a um outro de um aeroporto por uma esteira. Em um certo local a esteira tem uma inclinação de 2,5 ° com a horizontal. Suponha que para ângulo tão pequeno as mala
Um bloco começa a subir um plano inclinado sem atrito com uma velocidade inicial v 0 = 3,50m / s . O ângulo do plano inclinado é θ = 32,0 ° . (a) Que distância ao longo do plano inclinado o bloco cons