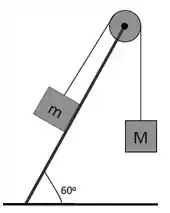
No plano inclinado abaixo, qual a massa necessária para deixar o sistema em equilíbrio, na ausência de atrito?
(a)
(b)
(c)
(d)
(e)
Dado: ;
Passo 1
Nosso objetivo é achar a massa para que esse negócio fique em equilíbrio.
Então, basta analisar as forças em cada um dos blocos, lembrando que a tração no cabo vai ser a mesma nos dois casos, já que tanto a polia quanto o cabo são ideais (enunciado não disse nada).
Passo 2
Vamos analisar primeiro o bloco de massa :
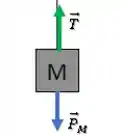
Se o sistema está em equilíbrio:
Agora, dá uma olhada no bloco de massa , lembrando que não temos atrito:
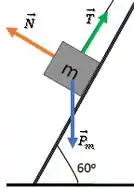
Pra aplicar a segunda lei de Newton, precisamos decompor aquela força peso , né?
Então, vamos achar alguma relação com essa inclinação da rampa.
A força tração é na mesma direção da rampa, então sua inclinação com a horizontal é:
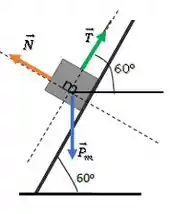
Agora, dá uma olhada nos ângulos e :
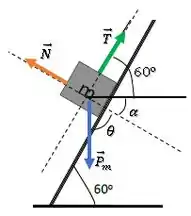
Os eixos em pontilhado (normal e paralelo à rampa) fazem entre si, então:
Mas, a força peso e a horizontal também têm um ângulo de entre si, por isso:
Agora, fica molhe decompor a força peso:
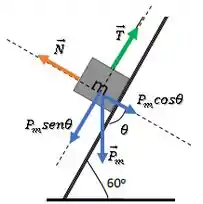
Bom, no outro bloquinho achamos uma relação para a força de tração , então vamos analisar o equilíbrio desse bloquinho na direção da rampa:
Já achamos que :
Passo 3
Pra finalizar, é só juntar as equações dos dois blocos e achar a massa :
A questão dá que :
Achamos que a nossa resposta é (a).
Resposta
Letra (a)