A Fig. 5-60 mostra parte de um teleférico. A massa máxima permitida de cada cabina com passageiros é de . As cabinas que estão penduradas em um cabo de sustentação, são puxadas por um segundo cabo ligado à torre de sustentação de cada cabina. Suponha que os cabos estão esticados e inclinados de um ângulo . Qual é a diferença entre as tensões de partes vizinhas do cabo que puxa as cabines se as cabinas estão com a máxima massa permitida e estão sendo aceleradas para cima a .

Passo 1
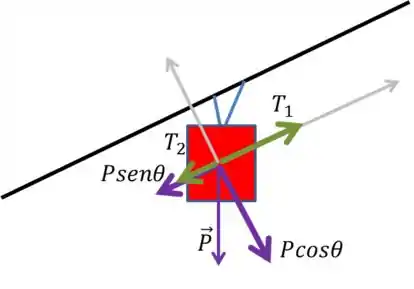
Nesse exercício, para reforçar mais ainda a ideia de usar os eixos na direção do movimento e perpendicular a ele, as trações, que constituem nosso objetivo, também estão na direção do movimento. Fazendo as decomposições na direção do movimento, já que as componentes no eixo normal não são interessantes para nós, temos:
Passo 2
Foi dada a aceleração das cabines, a massa delas e nós já temos as forças que agem na direção da aceleração, agora é só aplicar a segunda lei de Newton!
Substituindo os valores conhecidos:
E então:
Passo 3
Aí você me pergunta: Mas só foi calculada a diferença entre as trações da cabine do meio, não?
A resposta é: Sim. Fizemos a análise do movimento de somente uma cabine, mas, se formos fazer das outras, perceberemos que é idêntico. As cabines possuem as mesmas massas, sofrem ação de forças de mesma direção e ainda estão sob a mesma aceleração. Portanto, a resposta encontrada para uma cabine pode ser generalizada.