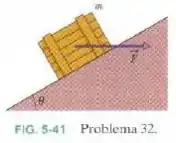
Na Fig. 5-41, um caixote de massa é empurrado por uma força horizontal que o faz subir uma rampa sem atrito () com velocidade constante. Quais são os módulos de e (b) da força que a rampa exerce sobre o caixote?
Passo 1
Para facilitar a análise do movimento mais facilmente, vamos estuda-lo nos dos eixos especiais: na direção do plano e perpendicularmente ao plano. Inicialmente as forças atuantes são essas aqui:
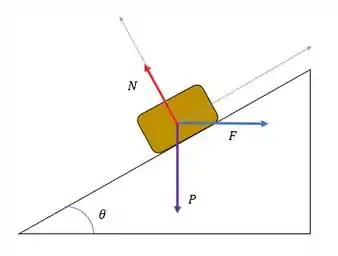
Decompondo as forças nos eixos especiais temos:
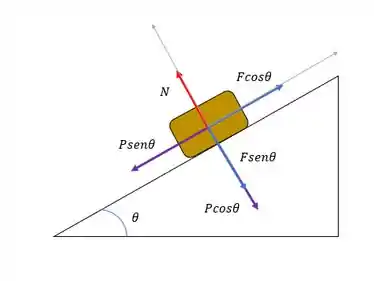
Uma parte importante do enunciado é que a caixa sobe a rampa com velocidade constante, ou seja, a resultante das forças na direção do plano é nula.
Passo 2
Vamos agora fazer o equilíbrio das forças no eixo paralelo ao plano já que é o que tem menos componentes e será mais fácil da gente analisar:
Vamos isolar a força
Onde a força peso é:
Como , podemos encontrar a força substituindo:
Passo 3
Agora que sabemos o valor de podemos encontrar a força normal ao plano fazendo o somatório das forças pro eixo perpendicular ao plano:
Substituindo os valores que a gente já calculou temos: