USP, Sem Campus, Física 1, Coletâneas de Exercícios - Parte I - Cinemática, Leis de Newton, Trabalho e Energia, Questão 37
37. Um corpo de massa está apoiado em um plano liso de inclinação , o qual tem uma aceleração que mantém o corpo estacionário em relação ao plano, como mostra a figura 2.10. Determinar esta aceleração. O que acontecerá se o plano tiver uma aceleração com módulo maior que o valor encontrado?
Passo 1
Iae, como vai? Essa questão está difícil, né? Fique tranquilo que vamos tentar te ajudar. 😎👍
Nesse problema temos um bloco de massa que está sob um plano inclinado que faz um ângulo com a horizontal. Esse plano possui uma aceleração e o que temos que fazer é obter a aceleração necessária para que o bloco permaneça parado e também temos que dizer o que acontece caso a aceleração aumente.
E aí, parece tranquilo? 🤔
Para que o bloco permaneça parado, deve haver um equilíbrio de forças que atuam sobre ele.
Como não há atrito, as únicas forças que atuarão no bloco são as forças peso , normal e a força devido a aceleração do plano.
Vamos começar desenhando o diagrama de forças do sistema.
Bora lá! 😐
Passo 2
A força normal sempre aponta perpendicularmente para cima do plano de contato, a força peso sempre aponta verticalmente para baixo e a força do movimento do plano aponta para o sentido oposto ao movimento pela inércia gerada por esse movimento já que quem acelera é o plano, ou seja
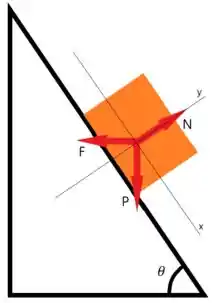
Vamos começar! Primeiro podemos desmembrar a força peso em duas partes, uma que aponta no sentido do eixo negativo e outra componente que aponta para o eixo positivo.
Por relações de triângulos, podemos descobrir que o ângulo entre e o semieixo negativo de é e portanto, o ângulo entre e o semieixo positivo de é
Fazendo a mesma análise para a força temos que o ângulo entre e o semieixo negativo de é e de para o semieixo negativo de é
Tranquilo até aqui? 😉
Passo 3
Para responder nossa pergunta, temos que analisar as forças que atuam no eixo , pois é esse eixo que determina se o bloco sobe ou desce.
Igualando as duas forças que atuam nesse sentido, vamos obter
A força nada mais é que a aceleração multiplicada pela massa do bloco
Já a força peso é dada por
Substituindo na equação e isolando
Considerando e foi dado como , então
E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí
