UFJF, Sem Campus, Física 1, AV1 - 2016.1, Questão 4b
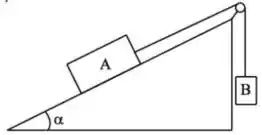
[4] A figura abaixo mostra uma caixa com massa que está apoiada sobre um plano inclinado que faz um ângulo com a horizontal. Esta caixa está amarrada, via uma corda sem massa e inextensível, a uma outra caixa de massa . A polia pela qual passa a corda é considerara como ideal. Os coeficientes de atrito estático e cinético entre e a superfície do plano inclinado são e , respectivamente.
(b) Ache a expressão do módulo da aceleração da caixa em função dos parâmetros dados no enunciado.
Passo 1
Fala aí, querido!! Tudo certinho? Bora resolver esse probleminha? 😉
Nesse problema temos uma caixa de massa e uma caixa de massa , ambas as caixas estão ligadas por uma corda perfeita que passa por uma polia também perfeita. A caixa está sob um plano inclinado e começa a subir o plano enquanto a caixa está pendurada pela corda no outro lado da polia.
Sabendo que possui atrito entre a caixa e o plano, queremos obter o modulo da aceleração da caixa .
Parece tranquilo? 😐
Para obter a aceleração da caixa temos que obter a força resultante na caixa e a partir daí aplicar a segunda lei de Newton
Bora começar! 😉
Passo 2
Vamos obter a força resultante em . Nessa orientação, temos a ação da força de atrito, a tração e uma parcela da força peso.
A força de tração é calculada como
Já a normal é obtida a partir da componente perpendicular á superfície da força peso, ou seja, se a superfície possui um ângulo com a horizontal, então a componente da força peso perpendicular a superfície é
Então a força de atrito é dada por
Da mesma forma podemos obter a componente da força peso paralela a superfície...
Bacana, não é? 😉
Passo 3
Agora temos que analisar como a força da corda atua na caixa.
Sabemos que , assim, fazemos e é dada pala força gravitacional menos a aceleração do sistema, ou seja
A força resultante no sentido positivo de pode ser calculado como o somatório das forças que atuam nessa direção, menos as forças que atuam na direção oposta, ou seja
Aplicando a segunda lei de Newton, temos
Isolando ...
Sacou como faz? Responde Aí! 😉
