Um vagão de massa está sobre um plano inclinado de inclinação , ligado a uma esfera suspensa, de massa , pelo sistema de cabos e polias ideais, como ilustrado na figura O coeficiente de atrito cinético entre o vagão e o plano inclinado é e o sistema é solto do repouso.
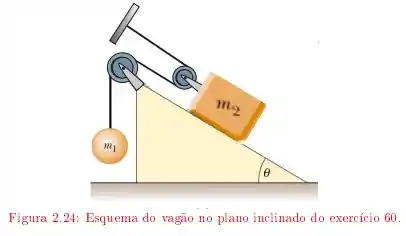
b) Utilizando a conservação da energia, calcule de que distância o vagão terá se deslocado, ao longo do plano inclinado, quando sua velocidade atingir
Passo 1
E aí pessoal, tudo certo com vocês?
Nessa questão temos um sistema de blocos, polias e plano inclinado, igual foi mostrado na figura. Basicamente, o bloco ou a esfera irá começar a descer enquanto o outro elemento irá subir. Como eles estão conectados por fio, deve haver um vínculo geométrico relacionando o movimento da esfera e do vagão.
No item anterior, usamos o vínculo geométrico da figura para determinar as seguintes relações:
Agora, o enunciado nos pede para determinar o deslocamento do vagão, ao longo do plano inclinado, quando sua velocidade for:
Nesse sistema, como temos força de atrito no vagão, a energia mecânica do sistema não se conserva. Mas, podemos usar o princípio do trabalho das forças não-conservativas para resolvê-lo. Esse princípio diz que:
(Considerando o sistema composto pela esfera e pelo vagão, a tração é como uma força interna e seu trabalho é nulo no sistema).
Vem com a gente que vamos explicar direitinho como aplicar essas ideias 😊
Passo 2
Bom pessoal, das relações que encontramos no item anterior, se o deslocamento do vagão é , podemos escrever que:
Da mesma forma, se:
Para aplicar a equação da conservação da energia é importante passarmos a unidade da velocidade para , basta dividir por . Assim:
Analogamente:
Excelente!
Agora vamos pensar no princípio do trabalho das forças não conservativas.
A única força não-conservativa que temos é a força de atrito. Do equilíbrio do vagão na direção perpendicular ao plano inclinado, temos:
Já quando à força de atrito cinético, temos:
Logo:
Assim, o trabalho da força de atrito vale:
Muito bom!
Passo 3
Já quanto à variação da energia mecânica, inicialmente o sistema está repouso, então:
Para escrever essa variação, podemos escrever:
Como a esfera deslocou-se para cima, a diferença de altura deve ser positiva.
E, o vagão deslocou-se no plano inclinado. Como foi descendo, essa diferença de altura deve ser negativa:
Sabendo também que:
Temos:
Igualando com o trabalho da força de atrito, vamos ter:
Isolando , temos:
Logo:
E é isso gente! Espero que vocês tenham entendido tudo bem direitinho!Até a próxima 😊