UFJF, Sem Campus, Física 1, AV1 - 2016.1, Questão 4c
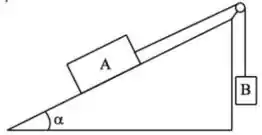
[4] A figura abaixo mostra uma caixa com massa que está apoiada sobre um plano inclinado que faz um ângulo com a horizontal. Esta caixa está amarrada, via uma corda sem massa e inextensível, a uma outra caixa de massa . A polia pela qual passa a corda é considerara como ideal. Os coeficientes de atrito estático e cinético entre e a superfície do plano inclinado são e , respectivamente.
(c) ache a expressão do modulo da tensão na corda em função dos parâmetros dados no enunciado.
Passo 1
E aí! Suave na nave?! Tá difícil essa questão? Relaxa que a gente vai te ajudar!
Nesse problema temos uma caixa de massa e uma caixa de massa , ambas as caixas estão ligadas por uma corda perfeita que passa por uma polia também perfeita. A caixa está sob um plano inclinado e começa a subir o plano enquanto a caixa está pendurada pela corda no outro lado da polia.
Sabendo que possui atrito entre a caixa e o plano, queremos obter o modulo tração na corda que liga as caixas.
Parece tranquilo? 😐
Se o sistema estivesse em repouso, a tração na corda seria igual a força peso da caixa .
Porém o sistema possui uma aceleração então essa aceleração amortece a tração que a corda sofre, então podemos definir que
Tranquilo até aqui? 👀
Passo 2
Anteriormente vimos que a aceleração do sistema é dada por
Antão podemos substituir em do passo 1 como
Simplificando um pouquinho...
O que achou? Foi de boa? Responde aí! 😊
