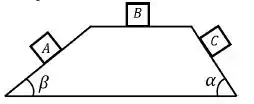
Três blocos, A, B e C de mesma massa repousam sobre as faces de um sólido formado de superfícies planas, como indicado na figura abaixo, onde e , . Considerando o módulo das forças normais exercida pelas superfícies sobre os blocos é correto afirmar que:
(a)
(b)
(c)
(d)
(e)
(f)
Passo 1
Vamos começar com o bloco .
No bloco , o diagrama de forças é bem tranquilo:
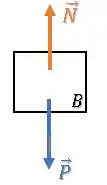
Como o bloco está em equilíbrio, temos:
Passo 2
Já no bloco e , temos um bloco num plano inclinado.
O diagrama de forças para o bloco fica:
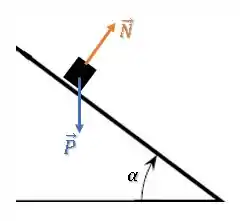
Mas agora, podemos decompor a força peso nas componentes paralela e perpendicular à rampa:
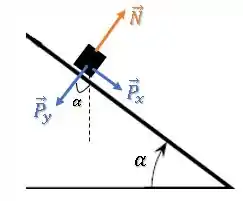
Aplicando a segunda lei de Newton na direção perpendicular à rampa, ainda temos um equilíbrio nessa direção:
Passo 3
Já o diagrama do bloco é semelhante ao do bloco , o que muda é o lado da rampa e o ângulo de inclinação:
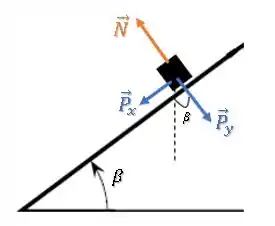
Aplicando a segunda lei do tio Newton, temos:
Passo 4
Ficamos com:
Todas elas são parecidas, sendo a única diferença aquele “cosseno”.
O cosseno dentro do intervalo ou é descrescente:
Ou seja, quanto maior for o ângulo de inclinação, menor será o “cosseno” desse ângulo e consequentemente, menor será a força normal atuando no bloco.
Então, a força normal no bloco é a maior delas.
Entre e , temos que olhar para seus ângulos.
O ângulo (bloco ) é maior que o ângulo (bloco ), portanto a relação entre os cossenos é inversa:
Assim:
Terminamos com:
Resumo da ópera... quanto menos inclinada for a rampa, maior a força normal sobre o bloco, sendo a inclinação nula (horizontal), o valor máximo de força normal.
Resposta
Letra (d)